Com os algarismos impares pode-se formar n numero maiores de 200 e que tenham apenas 3 algarismo distintos. O valor de n é:
A) 10
B) 48
C) 60
D) 72
E) 96
No gabarito esta como letra B, mas nao consegui chegar no resultado.



Souo escreveu:Com os algarismos impares pode-se formar n numero maiores de 200 e que tenham apenas 3 algarismo distintos. O valor de n é:
A) 10
B) 48
C) 60
D) 72
E) 96
No gabarito esta como letra B, mas nao consegui chegar no resultado.
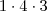 .
.

Voltar para Análise Combinatória
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: