Análise Combinatória

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Análise Combinatória

Regras do fórum
Responder

Análise Combinatória

Mensagempor thamysoares » Sex Jul 19, 2013 19:46

UFRJ - Uma pessoa possui 5 livros de física e 7 livros de matemática. De quantos modos distintos ela pode distribuir estes livros em uma estante de modo que dois ou mais livros de física nunca fiquem juntos?

Eu pensei em fazer assim:
M.F.M.F.M.F.M.F.M.F.M.M
7.5.6.4.5.3.4.2.3.1.2.1
Mas dá um número enorme e a RESPOSTA que está na minha apostila É: 56 :s

Me ajudem?
thamysoares
Usuário Ativo
Usuário Ativo
 
Mensagens: 23
Registrado em: Qua Nov 14, 2012 19:21
Formação Escolar: ENSINO MÉDIO
Andamento: cursando
Voltar ao topo

Re: Análise Combinatória

Mensagempor MateusL » Sex Jul 19, 2013 22:58

Pela resposta que está na apostila, deves considerar todos os livros de matemática idênticos, bem como todos os livros de física.

Primeiramente, coloque os 7 livros de matemática na estante, o que poderá ser feito de apenas um modo, pois todos os livros de matemática são idênticos. Agora terás 8 "vagas" para os livros de física: no início, entre o primeiro e o segundo livro de matemática, entre o segundo e o terceiro,..., entre o sexto e o sétimo ou no fim.

Como são cinco livros de física, deverás escolher cinco dentre as oito vagas disponíveis, o que dará:

{8\choose 5}=\dfrac{8!}{5!(8-5)!}=\dfrac{8\cdot 7\cdot 6}{3\cdot 2}=8\cdot 7=56

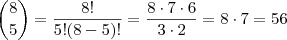
Abraço!
MateusL
Usuário Parceiro
Usuário Parceiro
 
Mensagens: 68
Registrado em: Qua Jul 17, 2013 23:25
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Elétrica
Andamento: cursando
Voltar ao topo
Responder

Voltar para Análise Combinatória

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo a=\sqrt{8}+ i em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja \alpha o ângulo entre o eixo horizontal e o afixo a. O triângulo é retângulo com catetos 1 e \sqrt{8}, tal que tg \alpha = \frac{1}{sqrt{8}}. Seja \theta o ângulo complementar. Então tg \theta = \sqrt{8}. Como \alpha + \theta = \frac{\pi}{2}, o ângulo que o afixo b formará com a horizontal será \theta, mas negativo pois tem de ser no quarto quadrante. Se b = x+yi, então \frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}. Como módulo é um: |b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}.

Logo, o afixo é b = \frac{1 + i\sqrt{8}}{3}.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum