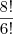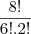Olá, pessoal.
"Um engenheiro fará uma passarela de 10m de comprimento, ligando a porta da casa ao portão da rua. A passarela terá 1m de largura e ele, para revestí-la, dispõe de 10 pedras quadradas de lado 1m e 5 pedras retangulares de 1m x 2m.
Todas as pedras são da mesma cor, as pedras de mesmo tamanho são indistinguíveis uma das outras e o rejunte ficará aparente, embora com espessura desprezível. De quantas maneiras ele pode revestir a passarela?"
A resposta é 89 possibilidades.
De fato, para o revestimento podem ser combinadas pedras (1x1, 1x2), apenas nas seguintes quantidades: (10, 0), (8, 1), (6, 2), (4, 3), (2, 4) e (0, 5).
Para os casos (10, 0) e (0, 5) só existe uma forma de revestir a passarela em cada caso.
Já para os outros, estou com dificuldades em quantifivar as possíveis posições das pedras, sem contá-las exaustivamente.
Para o caso (8, 1), é fácil observar que são 9 possibilidades, alterando-se apenas a única pedra 2x1, mas para os demais.....
É sugerido utilizar combinações, de fato, para o caso (8, 1), 9 = C9,1. Aplicando esse processo nos demais casos, a resposta se verifica, mas não consegui entender o porque de se aplicar Combinação nesse contexto. Ou seja, como, no cenário contextualizado, as combinações das somas das pedras 1x1 e 1x2 utilizadas, tomadas n a n (n = nº de pedras 1x2 utilizadas em cada caso) resolvem o problema...
Aguardo. Grato.