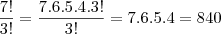por gustavowelp » Sex Nov 02, 2012 12:31
Caros amigos, não sei como resolver esta questão. Gostaria muito da ajuda de vocês. Obrigado!!!
No município de Sapucaia do Sul, uma das funções do técnico cultural é a divulgação de informações sobre a realização de atividades culturais. Sabendo-se que a quantidade de divulgações realizadas no 1º semestre de 2012 é equivalente ao número de anagramas que começam com a letra P e que podem ser formados com a palavra SAPUCAIA, pode-se afirmar que esse número corresponde a:
A resposta correta é 840.
Mas eu imaginei P _ _ _ _ _ _ _ e então 7! / 3! onde 3 é o número de repetições de A.
Obrigado pela ajuda.
Um abraço!!!
-
gustavowelp
- Usuário Parceiro
-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
por young_jedi » Sex Nov 02, 2012 12:46
é isso ai mesmo
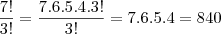
esta certo seu raciocinio
-
young_jedi
- Colaborador Voluntário
-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Anagrama Simples]
por gustavowelp » Sáb Ago 11, 2012 01:39
- 2 Respostas
- 1644 Exibições
- Última mensagem por gustavowelp
Qua Ago 15, 2012 23:48
Análise Combinatória
-
- Anagrama
por Igor » Sex Set 30, 2011 18:02
- 0 Respostas
- 1875 Exibições
- Última mensagem por Igor
Sex Set 30, 2011 18:02
Estatística
-
- [Anagrama]
por Geriane07 » Qui Ago 08, 2013 12:23
- 3 Respostas
- 1610 Exibições
- Última mensagem por DanielFerreira
Sáb Nov 02, 2013 09:06
Análise Combinatória
-
- Dúvida anagrama
por renataf » Ter Dez 07, 2010 08:47
- 2 Respostas
- 2211 Exibições
- Última mensagem por renataf
Dom Jan 02, 2011 13:45
Estatística
-
- Permutação-Anagrama
por Alessandra Cezario » Ter Jan 31, 2012 13:32
- 1 Respostas
- 1653 Exibições
- Última mensagem por Arkanus Darondra
Ter Jan 31, 2012 14:20
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
Resposta:
Dica:
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a
e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
