 por zenildo » Dom Jan 12, 2014 14:33
por zenildo » Dom Jan 12, 2014 14:33
DURANTE UMA REUNIÃO OCORREU UMA DIVERGÊNCIA QUANTO À FORMAÇÃO DE UMA COMISSÃO GESTORA, A SER ESCOLHIDA ENTRE OS PRESENTES. UM GRUPO DEFENDIA UMA COMISSÃO COM TRÊS MEMBROS, SENDO UM PRESIDENTE, UM VICE-PRESIDENTE E UM SECRETÁRIO. OUTRO GRUPO QUERIA UMA COMISSÃO COM TRÊS MEMBROS SEM CARGOS DEFINIDOS. A PRIMEIRA ALTERNATIVA OFERECE 280 POSSIBILIDADES DE ESCOLHA A MAIS QUE A SEGUNDA.
A) DETERMINE O NÚMERO DE PESSOAS PRESENTES À REUNIÃO, SABENDO-SE QUE ESSE NÚMERO É MAIOR QUE 5.
a resposta é 8
Sendo x(x - 1)(x- 2) = t »» t = t/6 + 280 »» 6t + t + 1680 »» 5t = 1680 »» t = 336 »» x(x - 1)(x - 2) = 336 »» Fatorando 336 = 16•3•7 = 8•7•6 »»
x(x - 1)(x - 2) = 8•7•6 »» x = 8.
Eu não consegui entender essa equação. Alguém poderia me explicar?
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por DanielFerreira » Ter Fev 18, 2014 11:16
por DanielFerreira » Ter Fev 18, 2014 11:16
Olá
Zenildo,
bom dia!
Inicialmente, deves saber que: o problema envolve um arranjo e uma combinação, respectivamente. Portanto, ficaria assim:

, onde "x" representa o número de pessoas presentes.
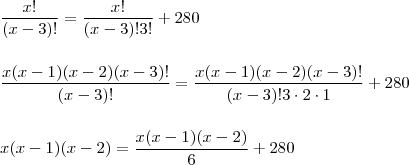
Espero ter ajudado!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (( Analise combinatória ))
por Roberta » Dom Jul 13, 2008 17:28
- 8 Respostas
- 15936 Exibições
- Última mensagem por Aparecida

Sáb Mai 05, 2012 00:07
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:20
- 4 Respostas
- 12204 Exibições
- Última mensagem por Neilson

Ter Mai 01, 2012 01:23
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:26
- 2 Respostas
- 8218 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 15, 2008 10:08
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:52
- 3 Respostas
- 7660 Exibições
- Última mensagem por Rejane Sampaio

Qui Set 25, 2008 10:43
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:56
- 2 Respostas
- 6402 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 22, 2008 11:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , onde "x" representa o número de pessoas presentes.
, onde "x" representa o número de pessoas presentes.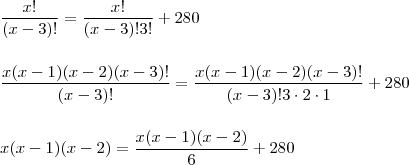


 .
.



