 por marinalcd » Qui Jul 30, 2015 16:07
por marinalcd » Qui Jul 30, 2015 16:07
Estou tentando resolver esta questão, mas estou com dificuldade. Alguém pode me ajudar?
Uma empresa de publicidade possui duas grandes contas. A conta de uma marca A de tênis e a conta de uma marca B de lingerie. Há 33 publicitários nesta empresa. Sabe-se que:
15 publicitários trabalham na conta da marca B de lingerie.
O número de publicitários que trabalham apenas na conta da marca A do tênis é quatro terços do número de publicitários que trabalham apenas na marca B de lingerie mais 3 publicitários.
O número de publicitários que não trabalham em nenhuma destas duas grandes contas é metade do número publicitários que trabalha em ambas as duas grandes contas.
a) Determine o número de publicitários que trabalham em ambas as duas grandes contas.
b) Determine o número de publicitários que trabalham apenas na conta da marca A do tênis.
c) Determine o número de publicitários que não trabalham em nenhuma das duas grandes contas.
Consegui determinar o número de publicitários que trabalham na conta A: 15.(4/3) + 3 = 23.
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por nakagumahissao » Sex Jul 31, 2015 12:14
por nakagumahissao » Sex Jul 31, 2015 12:14
Colegas, se alguém encontrar erros me corrijam por favor.
a) Determine o número de publicitários que trabalham em ambas as duas grandes contas.![n(A) = \frac{4}{3}n(B) + 3 = \frac{4}{3} 15 + 3 = 23\,\,\,\,\,\,\,\,\,\,[1] n(A) = \frac{4}{3}n(B) + 3 = \frac{4}{3} 15 + 3 = 23\,\,\,\,\,\,\,\,\,\,[1]](/latexrender/pictures/4e8ff0e053d98890648fcfab51cc9987.png)
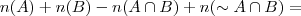
![= 23 + 15 - n(A \cap B) + n(\sim A \cap B)=33\,\,\,\,\,\,\,\,\,\,[2] = 23 + 15 - n(A \cap B) + n(\sim A \cap B)=33\,\,\,\,\,\,\,\,\,\,[2]](/latexrender/pictures/573ecafbca356c9b96bef63186e7ffaf.png)
Foi dado que:
![n(\sim A \cap B) = \frac{n(A \cap B)}{2}\,\,\,\,\,\,\,\,\,\,[3] n(\sim A \cap B) = \frac{n(A \cap B)}{2}\,\,\,\,\,\,\,\,\,\,[3]](/latexrender/pictures/00b03dd0f03116fac49815684abc8cf7.png)
Usando [3] em [2], teremos:


![n(A \cap B) = 10\,\,\,\,\,\,\,\,\,\,[4] n(A \cap B) = 10\,\,\,\,\,\,\,\,\,\,[4]](/latexrender/pictures/ec2b5a69ec9747a917abdb0cc8576b0d.png)
Resposta: 10
b) Determine o número de publicitários que trabalham apenas na conta da marca A do tênis.Este valor foi obtido em [1] acima e vale 23.
c) Determine o número de publicitários que não trabalham em nenhuma das duas grandes contas.Usando [4] obtido acima em [3] obtemos:

Resposta: 5 Publicitários
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [conjunto] dúvida numa questão da cespe
por Fabio Wanderley » Dom Abr 29, 2012 16:53
- 3 Respostas
- 2406 Exibições
- Última mensagem por MarceloFantini

Seg Mai 28, 2012 22:49
Conjuntos
-
- [conjunto] questão da PUC-SP
por Alane » Seg Ago 27, 2012 09:45
- 4 Respostas
- 4852 Exibições
- Última mensagem por MarceloFantini

Ter Ago 28, 2012 00:37
Conjuntos
-
- Resolução de Questão de Conjunto
 por marcone » Dom Abr 15, 2012 19:48
por marcone » Dom Abr 15, 2012 19:48
- 3 Respostas
- 3230 Exibições
- Última mensagem por DanielFerreira

Dom Abr 15, 2012 20:35
Conjuntos
-
- [conjunto solução em R] Questão Colégio Naval 2010
por Joan » Sáb Jul 23, 2011 12:06
- 2 Respostas
- 5386 Exibições
- Última mensagem por Joan

Sáb Jul 23, 2011 13:21
Equações
-
- Dúvida nessa de conjunto
 por igorcalfe » Qua Dez 28, 2011 19:16
por igorcalfe » Qua Dez 28, 2011 19:16
- 2 Respostas
- 1346 Exibições
- Última mensagem por fraol

Qua Dez 28, 2011 22:01
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![n(A) = \frac{4}{3}n(B) + 3 = \frac{4}{3} 15 + 3 = 23\,\,\,\,\,\,\,\,\,\,[1] n(A) = \frac{4}{3}n(B) + 3 = \frac{4}{3} 15 + 3 = 23\,\,\,\,\,\,\,\,\,\,[1]](/latexrender/pictures/4e8ff0e053d98890648fcfab51cc9987.png)
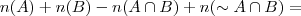
![= 23 + 15 - n(A \cap B) + n(\sim A \cap B)=33\,\,\,\,\,\,\,\,\,\,[2] = 23 + 15 - n(A \cap B) + n(\sim A \cap B)=33\,\,\,\,\,\,\,\,\,\,[2]](/latexrender/pictures/573ecafbca356c9b96bef63186e7ffaf.png)
![n(\sim A \cap B) = \frac{n(A \cap B)}{2}\,\,\,\,\,\,\,\,\,\,[3] n(\sim A \cap B) = \frac{n(A \cap B)}{2}\,\,\,\,\,\,\,\,\,\,[3]](/latexrender/pictures/00b03dd0f03116fac49815684abc8cf7.png)


![n(A \cap B) = 10\,\,\,\,\,\,\,\,\,\,[4] n(A \cap B) = 10\,\,\,\,\,\,\,\,\,\,[4]](/latexrender/pictures/ec2b5a69ec9747a917abdb0cc8576b0d.png)


 .
.



