 por Guga1981 » Qua Fev 11, 2015 19:32
por Guga1981 » Qua Fev 11, 2015 19:32
Amigos, não entendi o enunciado deste exercício.
Como um número x somado a um número y pode ser igual ao número y vezes o número x (afirmativa II)? Isso só da certo para x e y = 2 ou x e y = 1 e não para quaisquer x e y, como o exercício afirma.
Segue o exercício:
(U.E.CE 1980) Seja F :



uma função satisfazendo as seguintes propriedades:
I - f(0) = 1
II - f(x + y) = f(x) . f(y)

x, y


III - 0 < f(1) < 1
Então o valor da expressão f(0) + f(1) + f(2) + ... + f(9) é igual a:
a)
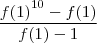
b)
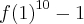
c)
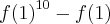
d)
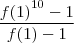
-
Guga1981
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Dom Jan 18, 2015 13:27
- Localização: São Vicente-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
-
 por Baltuilhe » Qua Fev 11, 2015 20:07
por Baltuilhe » Qua Fev 11, 2015 20:07
Boa tarde!
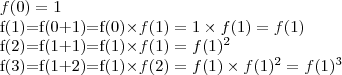
Então:
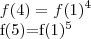
E assim sucessivamente.
Portanto, é uma P.G. com termo inicial 1 e razão f(1)
Fórmula da soma de P.G.
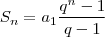
Onde q é a razão da P.G.
Substituindo o que se deve, então:
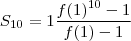
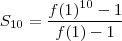
Como 0<f(1)<1 não há perigo em dar zero no denominador.
Espero ter ajudado!
-
Baltuilhe
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Dom Mar 24, 2013 21:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- pode me ajudar
por johnny » Sex Out 22, 2010 17:59
- 3 Respostas
- 1968 Exibições
- Última mensagem por Neperiano

Seg Out 25, 2010 21:19
Cálculo: Limites, Derivadas e Integrais
-
- Alguém pode corrigir?
por Giles » Sex Nov 07, 2008 09:06
- 6 Respostas
- 7382 Exibições
- Última mensagem por Giles

Sex Nov 07, 2008 19:48
Estatística
-
- Alguem pode ajudar-me?
por carlos r m oliveira » Seg Out 05, 2009 11:35
- 1 Respostas
- 2552 Exibições
- Última mensagem por Neperiano

Dom Jul 03, 2011 21:05
Estatística
-
- Quem pode me ajudar?
por Livia Primo » Ter Fev 02, 2010 18:44
- 2 Respostas
- 4099 Exibições
- Última mensagem por Livia Primo

Qua Fev 03, 2010 22:22
Funções
-
- Alguém pode me ajudar?
por apoliveirarj » Seg Jul 19, 2010 18:20
- 1 Respostas
- 3393 Exibições
- Última mensagem por Douglasm

Seg Jul 19, 2010 18:49
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 uma função satisfazendo as seguintes propriedades:
uma função satisfazendo as seguintes propriedades: x, y
x, y 

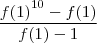
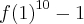
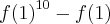
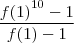


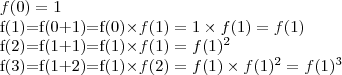
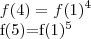
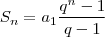
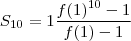
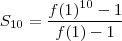


 , avisa que eu resolvo.
, avisa que eu resolvo.

