cardinalidade de N

[norberto]

Oi luiz.

Talvez isso fique mais claro :

- Seja r a grandeza que você batizou de "variação entre quantidades de casa"

O que podemos afirmar de r ?

Certamente, que r é uma grandeza finita. E isto se dá do fato de r representar a diferença entre dois números finitos. Assim como "números de casas", o conjunto de todas as grandezas r está limitado por "número finito de variação". Ou seja, tanto faz se tomarmos r, "número finito de casas", número de elementos da sequência, etc. etc. São todos redutíveis ao mesmo tipo de problema. Ficar mudando a descrição desse mesmo tipo de problema, pode ser chamado de "andar em círculos", pois todas as abordagens, devem, necessariamente, nos levar às mesmas conclusões. Nesse caso, a de que uma grandeza limitada, não pode variar ilimitadamente.

Abraços.

[norberto]

Oi Luiz !

Olha outra coisa que tá me incomodando.
Utilizamos 10 símbolos para representar os naturais. Mas sabemos que podemos construir um sistema numérico
com mais símbolos, tal como o sistema hexadecimal, que usa 16.
O Montequio sugere que imaginemos um sistema com "infinitos" símbolos.
Quantos dígitos seriam necessários para "enumerar" todos os reais ?

Exatamente 1.

O que seriam então os números formados com mais de um dígito, tal como 11, 27, 4A32Z, etc ?
Putz ! Minha cabeça tá em parafuso !


Abraços.

[LuizAquino]

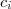Não, Luiz. Isso só nos remete para o que já concordamos. Que não existe um no conjunto de "número de casas" que seja o último elemento. Mas os elementos deste conjunto, não crescem "ilimitadamente". Eles crescem de acordo com a limitação de serem todos "números finitos de casas". O que não acontece com o conjunto "número de casa decimais".

Ok. Você continua achando que a quantidade de casas varia limitadamente entre os termos. Pois muito bem. Escolha um termo qualquer dessa sequência. Você consegue obter outro termo que tenha 1 casa a mais do que ele? E um outro que tenha 1 trilhão de casas a mais do que ele?

Ora, dado um termo qualquer dessa sequência sempre podemos obter um outro que tenha k casas a mais do que ele. Além disso, não há um valor máximo para esse número k. A conclusão disso é evidente: não há um máximo para o quanto a quantidade de casas pode variar.

Em resumo, podemos tanto ter termos com 1 casa de diferença quanto com 1 trilhão (ou mais) de casas de diferença.

Além disso, eu gostaria (sinceramente) de lhe fazer uma sugestão. Já que você está tão curioso sobre esses assuntos, que tal procurar um especialista? Procure por um professor especialista em teoria dos números no departamento de matemática da universidade mais próxima de onde você mora. Ou ainda, pesquise nas páginas das universidades por esses professores. Eles são as pessoas mais indicadas para finalmente lhe tirar todas essas dúvidas. Ou ainda, quem sabe, lhe deixar com tantas outras!

[norberto]

Em resumo, podemos tanto ter termos com 1 casa de diferença quanto com 1 trilhão (ou mais) de casas de diferença.

Ok ! Você continua acreditando que r, ou "diferença no número de casas" é um grandeza que varia "ilimitadamente". Essa diferença pode ser de 1, 1 trilhão, 1 gugol, 1 gugolplex. O fato de uma grandeza poder assumir valores enormes, não significa que ela é ilimitada. No caso de r ela não pode assumir "qualquer valor". Ela só pode assumir valores finitos. A grandeza d representando "diferença no número de casas decimais", essa sim, pode assumir qualquer valor.
Imagine um conjunto formado por todos os r e um formado por todos os d.

Qualquer que seja um elemento de r, não se pode pensar em um elemento de d que seja maior que ele. Isso significa que r > d ?
Qualquer que seja um elemento de d, não podemos imaginar um elemento de r maior que ele. As duas constatações significam que
os conjuntos são do mesmo tamanho ?



Dito de outra forma. Uma grandeza que só pode assumir valores finitos, é potencialmente infinita. Mas é finita.

Abraços.

Humpf ! Esquece o post seguinte. Só percebi que a gente podia podia alterar as mensagens depois de perceber que tua resposta tinha sido uma
e agora era outra.

É que eu tinha escrito :


Qualquer que seja um elemento de d, não podemos imaginar um elemento de d maior que ele. As duas constatações significam que os conjuntos são do mesmo tamanho ?

[norberto]

Oi luiz !

Desculpe, mas escrevi errado. O que quis escrever era :


Qualquer que seja um elemento de r, não se pode pensar em um elemento de d que seja maior que ele. Isso significa que r > d ?
Qualquer que seja um elemento de d, não podemos imaginar um elemento de r maior que ele. As duas constatações significam que
os conjuntos são do mesmo tamanho ?


Abraços.

[dmeneiz]

Amigos qual foi a conclusão ? eu acho que todos tem alguma razão. to certo ?