 por Neperiano » Ter Mar 09, 2010 14:44
por Neperiano » Ter Mar 09, 2010 14:44
Ola
Bom temos três numeros, e do lado temos as condições, então para se ter certeza disso necessitamos igualar o numero que esta embaixo, então:
108, 180, 300, divide por 2
,54, ,90, ,150, divide por 2
.27, ,45, ,75,, divide por 3
.09, ,15, ,25,, divide por 3
,03, ,05, ,25,, divide por 3
,01, ,05, ,25,, divide por 5
,01, ,01, ,05,, divide por 5
,01, ,01, ,01,, divide por 1
Multiplica todos = 2700, esse é o denominador comum entre os 3,
4/108<7/180<11/300
2700
Multiplique o denominador e depois multiplique
72900<220909,09<73636,36
Logo descobrimos que:
x=7\180
y=4\108
z=11\300
Por isso que devemos fazer o MMC, para podermos descubrir um denominador comum entre eles e descubrir cada valor, se você apenas dividisse, exemplo: 7\180 = 0,038888, 11/300=0,03666, repare que as posições de x,y e z, se inverteriam, isto se deve ao fato de elas não estarem igualadas, por isto se deve fazer o mmc, para descubrir quem é o x,y e z.
Qualquer duvida
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"



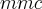 serve para você encontrar um denominador comum entre frações para que dessa maneira possa por exemplo somar, subtrair, comparar. Fiz dessa maneira e espero que você entenda:
serve para você encontrar um denominador comum entre frações para que dessa maneira possa por exemplo somar, subtrair, comparar. Fiz dessa maneira e espero que você entenda: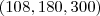 em números primos. Cheguei que:
em números primos. Cheguei que: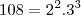
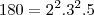
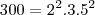
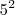 :
:
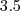 :
:
 :
:
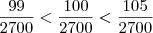 e
e  , vemos que:
, vemos que:
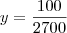
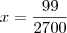




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.