 por Drakangt » Qui Jan 01, 2015 14:04
por Drakangt » Qui Jan 01, 2015 14:04
Olá tenho uma duvida nestes dois exercícios.
Faça a demonstração ou dê um contra-exemplo para cada umas das "propriedades seguintes
a C_ c ^ b C_ D----> axb = cxd
a U b C_ a (interseção) b -----> a=b
C_= contido
U= união
-
Drakangt
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Dez 29, 2014 14:28
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informatica e comunicações
- Andamento: cursando
 por adauto martins » Sex Jan 02, 2015 14:44
por adauto martins » Sex Jan 02, 2015 14:44
b)seria isso?...

seja
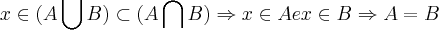
...
a)nao entendi bem...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Drakangt » Sex Jan 02, 2015 16:03
por Drakangt » Sex Jan 02, 2015 16:03

b)
-
Drakangt
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Dez 29, 2014 14:28
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informatica e comunicações
- Andamento: cursando
 por adauto martins » Sex Jan 02, 2015 18:12
por adauto martins » Sex Jan 02, 2015 18:12

seja
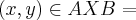
{

}...
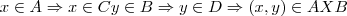
,logo
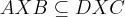
...mas o contrario nao podemos ter,pois podemos ter
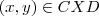
tal q.

...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Drakangt » Sex Jan 02, 2015 19:39
por Drakangt » Sex Jan 02, 2015 19:39
Logo é verdadeira certo?
Já agora a B) ii (a de baixo) utiliza-se alguma regra?
-
Drakangt
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Dez 29, 2014 14:28
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informatica e comunicações
- Andamento: cursando
 por Drakangt » Sáb Jan 03, 2015 12:55
por Drakangt » Sáb Jan 03, 2015 12:55
a b) ii seria um circulo dentro do outro pk são iguais.
-
Drakangt
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Dez 29, 2014 14:28
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informatica e comunicações
- Andamento: cursando
 por adauto martins » Sáb Jan 03, 2015 14:31
por adauto martins » Sáb Jan 03, 2015 14:31
circulo?...nao se definiu os elementos dos conjuntos...
ii)p/ vc mostrar q. A=B,tem-se q. mostrar q.
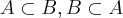
a proposiçao eh:
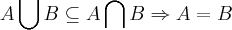
entao vamos tomar um elemento
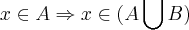
,como foi dado q.

,logo

...analogo p/

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [conjutos]uepa 2014
por mmoreiraellen » Qua Fev 26, 2014 11:52
- 1 Respostas
- 15801 Exibições
- Última mensagem por pamelacarolinne

Seg Mai 12, 2014 10:38
Conjuntos
-
- Algebra Linear para resolução de Conjutos
por SuPr3MeMoTF » Qui Out 15, 2015 17:11
- 1 Respostas
- 2074 Exibições
- Última mensagem por adauto martins

Qui Out 15, 2015 19:11
Álgebra Linear
-
- [Dúvida ANOVA] Uma dúvida sobre a estatística correta
por gustamfar » Ter Mai 22, 2018 18:19
- 0 Respostas
- 11054 Exibições
- Última mensagem por gustamfar

Ter Mai 22, 2018 18:19
Estatística
-
- Dúvida PA
por Cleyson007 » Dom Jun 01, 2008 01:01
- 2 Respostas
- 10764 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Progressões
-
- Dúvida
por miguelbaptista » Sex Jan 09, 2009 03:29
- 8 Respostas
- 12526 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:13
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




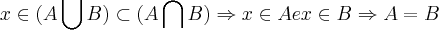 ...
...


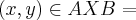 {
{ }...
}...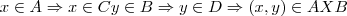 ,logo
,logo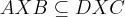 ...mas o contrario nao podemos ter,pois podemos ter
...mas o contrario nao podemos ter,pois podemos ter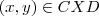 tal q.
tal q.  ...
...


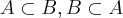
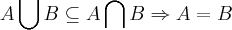
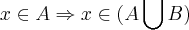 ,como foi dado q.
,como foi dado q.  ,logo
,logo  ...analogo p/
...analogo p/
