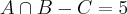por vinicius gouveia » Seg Dez 23, 2013 22:17
por vinicius gouveia » Seg Dez 23, 2013 22:17
OBSERVE ESTES CONJUNTOS DE NUMEROS NATURAIS:
A={4,5,8,9}
B={5,6,7,8}
C={1,7,8,9}
AS ALTERNATIVAS A SEGUIR CORRESPONDEM À OPERAÇÕES REALIZADAS COM OS REFERIDOS CONJUNTOS, IDENTIFIQUE QUAL DELAS ESTÁ INCORRETA:
a)
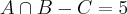
b)

c)

d)

e)

URGENCIA NA RESPOSTA,POIS DEPENDENDO DA RESPOSTA AQUI, ENTRO COM RECURSO ATE AMANHA QUE É O PRAZO!
-
vinicius gouveia
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Dez 23, 2013 22:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: cursando
 por young_jedi » Seg Dez 23, 2013 23:09
por young_jedi » Seg Dez 23, 2013 23:09
acredito que a alternativa falsa seja a c)
a intersecção das tres daria {8}
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- PRECISO DA RESPOSTA URGENTE
por trix17 » Qua Nov 09, 2011 23:34
- 0 Respostas
- 1394 Exibições
- Última mensagem por trix17

Qua Nov 09, 2011 23:34
Trigonometria
-
- a sua resposta!!
por weverton » Seg Jul 12, 2010 18:44
- 1 Respostas
- 1375 Exibições
- Última mensagem por weverton

Seg Jul 12, 2010 19:22
Progressões
-
- Nao comsegui axa a resposta ...
por jean » Sáb Nov 29, 2008 17:44
- 2 Respostas
- 2026 Exibições
- Última mensagem por jean

Sáb Nov 29, 2008 21:45
Pedidos
-
- Discordância de resposta
por timoteo » Qua Abr 10, 2013 13:02
- 3 Respostas
- 2753 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 21:22
Estatística
-
- dúvida na resposta
por Anderson Claiton 77 » Dom Ago 23, 2015 12:41
- 1 Respostas
- 1360 Exibições
- Última mensagem por Matpas

Qui Ago 27, 2015 17:55
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.