Ai galera, to com uma duvida no seguinte exercicio, do PSACN 2007, eu encontrei letra c como resposta, nao concorda com o gabarito pois diz que é a letra e , gostaria da ajuda da galera ai =D
PSACN 2007 - Em uma classe de x alunos, o professor de matemática escreveu, no quadro de giz, um conjunto A de n elementos.A seguir, pediu que, por ordem de chamada, cada aluno fosse ao quadro e escrevesse um subconjunto de A, diferente dos que já foram escritos. Depois de cumprirem com a tarefa, o professor notou que ainda existiam subconjuntos que nao haviam sido escritos pelos alunos. Passou a chamá-los novamente, até que o 18° aluno seria obrigado a repetir um dos subconjuntos já escritos. O valor mínimo de x, que atende às condições dadas, está entre
(a)24 e 30
(b)29 e 35
(c)34 e 40
(d)39 e 45
(e)44 e 50
bom, eu entendi o raciocinio do problema mais nao consegui por em pratica, fiz alguns calculos e achei 34,35, gostaria da opinião do pessoal ai ^^
VLww abç


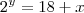




 , avisa que eu resolvo.
, avisa que eu resolvo.

