 por Vinicius » Dom Abr 05, 2009 17:12
por Vinicius » Dom Abr 05, 2009 17:12
Numa escola de Salvador 56 alunos lêem o jornal A, 21 lêem os jornais A e B, 106 lêem apenas um dos jornais e 66 não lêem o jornal B. Quantos alunos estudam na escola?
Resposta > 158 alunos
Provavelmente é de fácil solução para vocês, mas não consigo chegar no resultado, pois simplesmente no Diagrama de Venn não sei onde coloco os 106 alunos e os 66 alunos, estou frustrado por não saber resolver esta questão, me ajudem.
Obrigado.
-
Vinicius
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Abr 05, 2009 16:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração de Empresas
- Andamento: formado
 por admin » Dom Abr 05, 2009 18:38
por admin » Dom Abr 05, 2009 18:38
Olá Vinicius, boas-vindas!
Precisamos pensar em outro conjunto que não está sendo citado, disjunto, que envolve aqueles que não leem A nem B.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Vinicius » Dom Abr 05, 2009 20:30
por Vinicius » Dom Abr 05, 2009 20:30
Muito obrigado Fabio, então resolução seria:
A U B U C = 56+71+31 > 158.
Não me recordo do "disjunto"...não conseguiria resolver esta questão, pois no capítulo não tem uma explicação ou exemplo deste tipo de problema.
Imaginei que se 106 alunos lêem apenas um dos jornais, logo seria o jornal B, pois o nº de alunos do jornal A já esta quantificado. E se 66 alunos não lêem o jornal B, então quer dizer que eles lêem o jornal A, senão o enunciado seria que "66 alunos não lêem o jornal A e B". Raciocinei desta forma pois não tinha conhecimento do disjunto. Mas o meu raciocínio foi lógico?
-
Vinicius
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Abr 05, 2009 16:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração de Empresas
- Andamento: formado
 por admin » Dom Abr 05, 2009 21:03
por admin » Dom Abr 05, 2009 21:03
Vinicius, apenas note que:
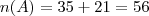
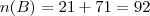
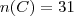
Dois conjuntos são disjuntos quando a intersecção é o conjunto vazio.
Não há apenas uma forma de escrever a resolução, mas veja algumas para auxiliar o entendimento:

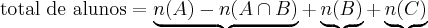
Ou pensando nas 4 partes:

Mais resumidamente, usando união:
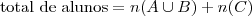
Ou ainda:
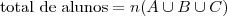
Espero ter ajudado!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Vinicius » Dom Abr 05, 2009 22:17
por Vinicius » Dom Abr 05, 2009 22:17
Foi bastante esclarecedor, muito obrigado pela sua atenção e espero contar com sua ajuda em outras dúvidas.
-
Vinicius
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Abr 05, 2009 16:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração de Empresas
- Andamento: formado
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Dúvida sobre conjuntos vazios
por ALPC » Qui Set 18, 2014 18:28
- 5 Respostas
- 6403 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 15:44
Conjuntos
-
- [Conjuntos] Problema de conjuntos com porcentagem
por Tibes » Qui Jan 31, 2013 14:29
- 1 Respostas
- 7951 Exibições
- Última mensagem por young_jedi

Sex Fev 01, 2013 12:39
Conjuntos
-
- Questao sobre conjuntos
por cadu » Ter Out 19, 2010 23:16
- 0 Respostas
- 1446 Exibições
- Última mensagem por cadu

Ter Out 19, 2010 23:16
Álgebra Elementar
-
- Questão do ITA sobre conjuntos!
por Abelardo » Qui Mar 03, 2011 02:03
- 5 Respostas
- 5423 Exibições
- Última mensagem por LuizAquino

Sex Mar 04, 2011 09:44
Álgebra Elementar
-
- Dúvida iniciante sobre conjuntos
por cassiosv13 » Sex Mar 09, 2012 01:45
- 1 Respostas
- 1650 Exibições
- Última mensagem por cassiosv13

Sex Mar 09, 2012 02:14
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



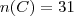

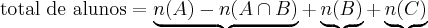

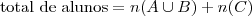
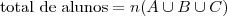

 .
.



