 por Mbssilva » Dom Fev 12, 2017 15:41
por Mbssilva » Dom Fev 12, 2017 15:41
Boa tarde amigos.
 http://prnt.sc/e7s4ri
http://prnt.sc/e7s4riNão conseguir desenvolver ela. Porém, acredito que a condição de existência eu tenha conseguido achar: {x ? ?|-1? x <0 ou x ?1}.
Como posso terminar essa conta??
Obrigado desde já àqueles que me ajudarem.
-
Mbssilva
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Fev 12, 2017 15:28
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por 314159265 » Seg Fev 13, 2017 06:01
por 314159265 » Seg Fev 13, 2017 06:01
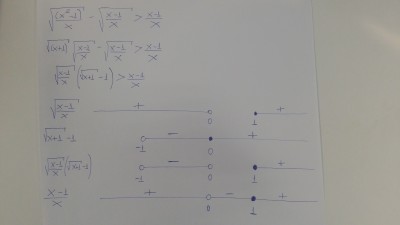
Eu tou tentando fazer sua questão, que realmente é complicada. Eu transformei a subtração do lado esquerdo em produto e fiz a análise do sinal das funções. Veja no anexo. Perceba que se x < 0, a inequação será sempre insatisfeita, pois negativo sempre vai ser menor do que positivo. Eu sei que minha solução está em x>=1 e sei também que pra x = 1 ela não é satisfeita, pois ambos os lados serão 0. Eu só não tou conseguindo provar que pra qualquer x > 1 a inequação é satisfeita. Pra isso eu só preciso provar que as curvas não se cruzam em x > 1.
- Anexos
-
-
314159265
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Fev 13, 2017 02:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por adauto martins » Qua Fev 15, 2017 17:09
por adauto martins » Qua Fev 15, 2017 17:09
racionalizar os radicais:
![(\sqrt[]{x-(1/x)}-\sqrt[]{1-(1/x)}).(\sqrt[]{x-(1/x)}+ (\sqrt[]{1-(1/x))} \succ ((x-1)/x).(\sqrt[]{x-(1/x)}+\sqrt[]{1-(1/x)} (\sqrt[]{x-(1/x)}-\sqrt[]{1-(1/x)}).(\sqrt[]{x-(1/x)}+ (\sqrt[]{1-(1/x))} \succ ((x-1)/x).(\sqrt[]{x-(1/x)}+\sqrt[]{1-(1/x)}](/latexrender/pictures/0913c92c8fde9c9c453c7053306aaf2a.png)

![x-(1/x)-(1-(1/x))\succ ((x-1)/x).(\sqrt[]{x-(1/x)}+\sqrt[]{1-(1/x)} x-(1/x)-(1-(1/x))\succ ((x-1)/x).(\sqrt[]{x-(1/x)}+\sqrt[]{1-(1/x)}](/latexrender/pictures/728a5a1447183949fed726b94f7ffb36.png)
...
![x-1\succ ((x-1)/x).(\sqrt[]{...}+\sqrt[]{...})\Rightarrow x\succ \sqrt[]{...}+\sqrt[]{...} x-1\succ ((x-1)/x).(\sqrt[]{...}+\sqrt[]{...})\Rightarrow x\succ \sqrt[]{...}+\sqrt[]{...}](/latexrender/pictures/91c7a4f450923491314fd113c9fce24e.png)
...ai é elevar ao quadrado ate tirar o radical,assim resolve-se a inequaçao...termine-o...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Inequações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Lógica e Conjuntos, questão cabulosa.
por legendandom » Qui Abr 15, 2010 15:50
- 1 Respostas
- 2703 Exibições
- Última mensagem por Neperiano

Ter Set 27, 2011 19:58
Álgebra Elementar
-
- questão cabulosa. Ajuda aqui!!!
por zenildo » Seg Mai 09, 2016 01:49
- 4 Respostas
- 3137 Exibições
- Última mensagem por zenildo

Qui Mai 12, 2016 22:43
Trigonometria
-
- [INEQUAÇÂO] Inequação do tipo: (a+ x < b + x < c + x)
por Diofanto » Dom Fev 03, 2013 19:55
- 7 Respostas
- 6296 Exibições
- Última mensagem por Diofanto

Qui Fev 14, 2013 23:45
Inequações
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7384 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- Inequação
por Luna » Seg Set 28, 2009 18:55
- 4 Respostas
- 3717 Exibições
- Última mensagem por Molina

Ter Set 29, 2009 16:50
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![(\sqrt[]{x-(1/x)}-\sqrt[]{1-(1/x)}).(\sqrt[]{x-(1/x)}+ (\sqrt[]{1-(1/x))} \succ ((x-1)/x).(\sqrt[]{x-(1/x)}+\sqrt[]{1-(1/x)} (\sqrt[]{x-(1/x)}-\sqrt[]{1-(1/x)}).(\sqrt[]{x-(1/x)}+ (\sqrt[]{1-(1/x))} \succ ((x-1)/x).(\sqrt[]{x-(1/x)}+\sqrt[]{1-(1/x)}](/latexrender/pictures/0913c92c8fde9c9c453c7053306aaf2a.png)

![x-(1/x)-(1-(1/x))\succ ((x-1)/x).(\sqrt[]{x-(1/x)}+\sqrt[]{1-(1/x)} x-(1/x)-(1-(1/x))\succ ((x-1)/x).(\sqrt[]{x-(1/x)}+\sqrt[]{1-(1/x)}](/latexrender/pictures/728a5a1447183949fed726b94f7ffb36.png) ...
...![x-1\succ ((x-1)/x).(\sqrt[]{...}+\sqrt[]{...})\Rightarrow x\succ \sqrt[]{...}+\sqrt[]{...} x-1\succ ((x-1)/x).(\sqrt[]{...}+\sqrt[]{...})\Rightarrow x\succ \sqrt[]{...}+\sqrt[]{...}](/latexrender/pictures/91c7a4f450923491314fd113c9fce24e.png) ...ai é elevar ao quadrado ate tirar o radical,assim resolve-se a inequaçao...termine-o...
...ai é elevar ao quadrado ate tirar o radical,assim resolve-se a inequaçao...termine-o...
