Vou resolver a primeira de uma forma diferente ,comente qualquer coisa .
Seja ,
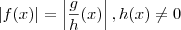
.
Onde :

e

.
Vamos obter os intervalor para as quais as funções

e

são positivas e negativas .
Temos :
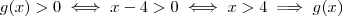
é positiva para todo

em

E ,
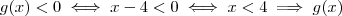
é negativa para todo x em
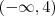
.
De forma análoga temos ,

é positiva para todo

em

E,
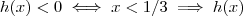
é negativa para todo

em
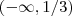
.
A conclusão é que quando

e

são simultaneamente positiva ou negativa ,vamos ter

estritamente positiva ,caso contrário

.
Mas perceba que não necessariamente todos elementos do domínio da função

pertence ao domínio da função

. (De modo que acontece os casos acima ) ;
Tomando a interseção ,segue que :
Para
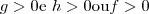

.
Para

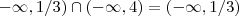
.
Já agora , veja :
Para
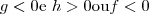

Para

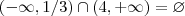
.
Com isso podemos reescrever a função

em sentença e retirar o seu modulo :
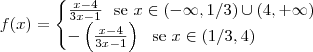
.
Conseguiu entender por que tivermos que fazer a interseção . Agora só resolver
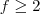
.
Caso 1 :


Agora note que qualquer
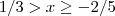
satisfaz
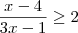
.
Como chegamos a este resultado , veja nossa condição :

.
Faça um teste , 1 > -2/5 .Mas 1 não satisfaz
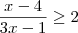
.(Reflita!) .
Agora tente concluir os casos 2 e 3 .
Caso 2 :
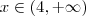
Caso 3:

É bem trabalhoso , mas acredito que é bem mais claro de compreender desta forma .Espero q ajude .
 .
.

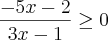
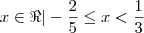 }
}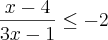


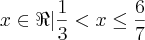 }
}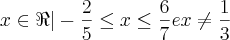 }
}



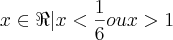 }
}


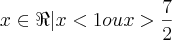 }
}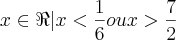 }
}

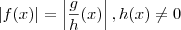 .
.  e
e  .
.  e
e  são positivas e negativas .
são positivas e negativas . 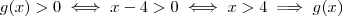 é positiva para todo
é positiva para todo  em
em 
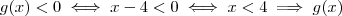 é negativa para todo x em
é negativa para todo x em 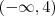 .
.  é positiva para todo
é positiva para todo 
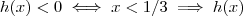 é negativa para todo
é negativa para todo 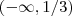 .
.  estritamente positiva ,caso contrário
estritamente positiva ,caso contrário  .
. 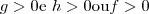
 .
. 
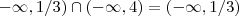 .
. 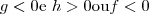


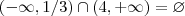 .
. 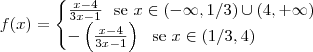 .
.  .
. 

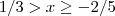 satisfaz
satisfaz 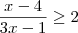 .
. 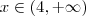

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.