 por Lenin » Qui Mai 30, 2013 21:17
por Lenin » Qui Mai 30, 2013 21:17
Pessoal, não lembro como resolver essas inequações do tipo:
1.

2.
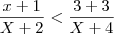
sei que é algo besta, mas não lembro como fazer...alguém poderia me ajudar?
-
Lenin
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 10, 2013 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
 por Rafael16 » Qui Mai 30, 2013 22:31
por Rafael16 » Qui Mai 30, 2013 22:31
Olá
Lenin!
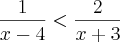

Aqui tem que tirar o mmc de expressões algébricas, caso não saiba, da uma pesquisada.

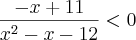
Chegamos em uma inequação quociente.
Vamos chamar o numerador de f(x) e denominador de g(x). Depois achar as raízes de cada função e fazer o estudo de sinais, que é o que faremos agora:

f(x) é uma função decrescente, ou seja, para valores de x acima de 11, a função vai ser negativa, e para valores de x abaixo de 11, positiva.
Vamos agora achar a raiz da função g(x) e fazer o estudo de sinais:

e

são as raízes.
g(x) é uma função com concavidade para cima, então para valores de x menor que -3, a função é positiva. Para valores de x maior que 4, a função também é positiva. E para valores de x entre -3 e 4, a função é negativa.
Depois é só fazer o jogo de sinais.
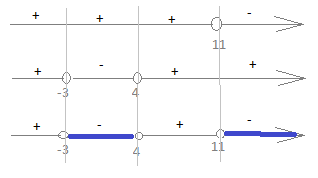
- JogoDeSinais.png (3.28 KiB) Exibido 5734 vezes
Essa é a solução
Qualquer dúvida comenta ai.
E tente fazer a 2.
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Lenin » Qui Mai 30, 2013 23:05
por Lenin » Qui Mai 30, 2013 23:05
Rafael16 escreveu:Olá
Lenin!
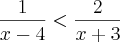

Aqui tem que tirar o mmc de expressões algébricas, caso não saiba, da uma pesquisada.

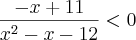
Chegamos em uma inequação quociente.
Vamos chamar o numerador de f(x) e denominador de g(x). Depois achar as raízes de cada função e fazer o estudo de sinais, que é o que faremos agora:

f(x) é uma função decrescente, ou seja, para valores de x acima de 11, a função vai ser negativa, e para valores de x abaixo de 11, positiva.
Vamos agora achar a raiz da função g(x) e fazer o estudo de sinais:

e

são as raízes.
g(x) é uma função com concavidade para cima, então para valores de x menor que -3, a função é positiva. Para valores de x maior que 4, a função também é positiva. E para valores de x entre -3 e 4, a função é negativa.
Depois é só fazer o jogo de sinais.
JogoDeSinais.png
Essa é a solução
Qualquer dúvida comenta ai.
E tente fazer a 2.
Ah sim..vlw..outra dúvida..se aqui nessa expressão

eu pegar o

e fazer por inequações-produto que no caso ficaria
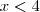
e

ao invés de ir para uma equação do segundo grau e calcular delta, poderia tbm né? ou não daria o mesmo resultado em todas? Abraços.
-
Lenin
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 10, 2013 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
 por Rafael16 » Qui Mai 30, 2013 23:27
por Rafael16 » Qui Mai 30, 2013 23:27
Lenin escreveu:Ah sim..vlw..outra dúvida..se aqui nessa expressão

eu pegar o

e fazer por inequações-produto que no caso ficaria
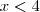
e

ao invés de ir para uma equação do segundo grau e calcular delta, poderia tbm né? ou não daria o mesmo resultado em todas? Abraços.
Sim, chegaríamos no mesmo lugar. Veja:



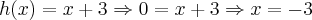
Jogando na reta para fazer o jogo de sinais, fica:

- JogoDeSinais2.png (2.8 KiB) Exibido 5729 vezes
Depois temos que fazer o jogo de sinais dessa reta com a reta do numerador.
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Lenin » Sáb Jun 01, 2013 01:00
por Lenin » Sáb Jun 01, 2013 01:00
Rafael16 escreveu:Lenin escreveu:Ah sim..vlw..outra dúvida..se aqui nessa expressão

eu pegar o

e fazer por inequações-produto que no caso ficaria
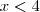
e

ao invés de ir para uma equação do segundo grau e calcular delta, poderia tbm né? ou não daria o mesmo resultado em todas? Abraços.
Sim, chegaríamos no mesmo lugar. Veja:



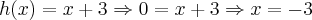
Jogando na reta para fazer o jogo de sinais, fica:
JogoDeSinais2.png
Depois temos que fazer o jogo de sinais dessa reta com a reta do numerador.
vlw brother..abração
-
Lenin
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 10, 2013 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
Voltar para Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

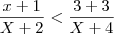


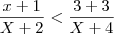

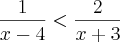


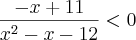

 e
e  são as raízes.
são as raízes.
e
são as raízes.
 eu pegar o
eu pegar o  e fazer por inequações-produto que no caso ficaria
e fazer por inequações-produto que no caso ficaria 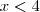 e
e  ao invés de ir para uma equação do segundo grau e calcular delta, poderia tbm né? ou não daria o mesmo resultado em todas? Abraços.
ao invés de ir para uma equação do segundo grau e calcular delta, poderia tbm né? ou não daria o mesmo resultado em todas? Abraços.
eu pegar o
e fazer por inequações-produto que no caso ficaria
e
ao invés de ir para uma equação do segundo grau e calcular delta, poderia tbm né? ou não daria o mesmo resultado em todas? Abraços.



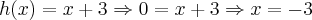

eu pegar o
e fazer por inequações-produto que no caso ficaria
e
ao invés de ir para uma equação do segundo grau e calcular delta, poderia tbm né? ou não daria o mesmo resultado em todas? Abraços.








