 por FuturoFuturista » Ter Jan 22, 2013 21:27
por FuturoFuturista » Ter Jan 22, 2013 21:27
1) Determine o conjunto solução:
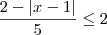
Tentei fazer assim:

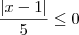
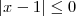
Minha conte deu isso

ou

só que no gabarito consta como solução igual o conjunto dos reais
onde eu errei?
-
FuturoFuturista
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Jan 22, 2013 20:59
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Química
- Andamento: cursando
 por e8group » Ter Jan 22, 2013 22:15
por e8group » Ter Jan 22, 2013 22:15
Sua solução não estar errada .Basta notar que se

e

, isto será o mesmo que ,
![x\in (-\infty , 1] \cup [ 1 , +\infty) x\in (-\infty , 1] \cup [ 1 , +\infty)](/latexrender/pictures/39664ce49ad71a7eb0118cc85d8f5526.png)
ou seja ,
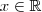
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Inequações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Inequação modular], alguem me ajuda por favor
por shyzum » Qua Mar 21, 2012 18:07
- 3 Respostas
- 2581 Exibições
- Última mensagem por MarceloFantini

Seg Abr 02, 2012 23:32
Sistemas de Equações
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 6484 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- Alguem me ajuda nessa equação exponencial
por raphael11234 » Qua Jun 08, 2016 00:07
- 1 Respostas
- 4720 Exibições
- Última mensagem por Cleyson007

Qua Jun 08, 2016 15:20
Equações
-
- Potenciação - Me ajudem nessa questão, por favor.
por Gabriel_DIT » Qua Fev 06, 2013 15:53
- 3 Respostas
- 2630 Exibições
- Última mensagem por DanielFerreira

Dom Fev 10, 2013 20:56
Aritmética
-
- [probabilidade] Ajudem nessa questão por favor
por amanda s » Sáb Nov 16, 2013 09:53
- 1 Respostas
- 1641 Exibições
- Última mensagem por DanielFerreira

Sex Nov 29, 2013 00:30
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
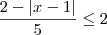

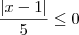
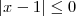
 ou
ou  só que no gabarito consta como solução igual o conjunto dos reais
só que no gabarito consta como solução igual o conjunto dos reais
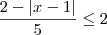

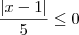
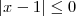
 ou
ou  só que no gabarito consta como solução igual o conjunto dos reais
só que no gabarito consta como solução igual o conjunto dos reais
 e
e  , isto será o mesmo que ,
, isto será o mesmo que , ![x\in (-\infty , 1] \cup [ 1 , +\infty) x\in (-\infty , 1] \cup [ 1 , +\infty)](/latexrender/pictures/39664ce49ad71a7eb0118cc85d8f5526.png) ou seja ,
ou seja ,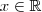

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)