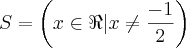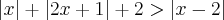

Se imaginarmos as funções modulares:
f(x) = |x|
g(x) = |2x + 1|
h(x) = |x - 2|
Veremos que o vértice de cada uma delas (já que a função se comporta como duas retas partindo de um vértice) é:
f(x) ---> 0
g(x) --->
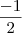
h(x) ---> 2
Agora, sabemos que a função f(x) é paralela à função h(x). Isso quer dizer que, não importa o quão grande sejam os valores de x, em certos intervalos, f(x) - h(x) terá o mesmo valor. Observe que no intervalo
![\left[2 ; \infty \right] \left[2 ; \infty \right]](/latexrender/pictures/883cfd4aa57f1f043a60ef5aca81fadb.png)
, ela se comportará dessa forma:
f(2) = 2
h(2) = 0
f(2) - h(2) = 2 em todo esse intervalo. Lá, a desigualdade está correta.
As funções também tem esse comportamento em
![\left[-\infty ; 0\right] \left[-\infty ; 0\right]](/latexrender/pictures/597f8ed77f3bb59a9ed041c91a948d26.png)
:
f(0) = 0
h(0) = 2
f(0) - h(0) = -2 em todo esse intervalo. Lá, a desigualdade está correta, exceto em x =
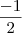
, já que a função g(x) é nula nele.
No entanto, devemos analizar as funções no intervalo

:
As funções f(x) e g(x) crescem lá, pois seus vértices são antes desse intervalo. Já a função h(x) decresce sempre, o que prova que o seu maior valor nesse intervalo é menor que h(0) = 2. Já os valores de f(0) = 0 e g(0) = 1.
Portanto, o menor valor dessa desigualdade no intervalo dado, seria maior que -1 que é maior que -2. Portanto é certo falar que o conjunto solução disso é:
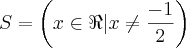




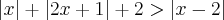

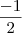
![\left[2 ; \infty \right] \left[2 ; \infty \right]](/latexrender/pictures/883cfd4aa57f1f043a60ef5aca81fadb.png) , ela se comportará dessa forma:
, ela se comportará dessa forma:![\left[-\infty ; 0\right] \left[-\infty ; 0\right]](/latexrender/pictures/597f8ed77f3bb59a9ed041c91a948d26.png) :
: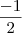 , já que a função g(x) é nula nele.
, já que a função g(x) é nula nele. :
: