 por Josemar » Dom Mar 25, 2018 22:33
por Josemar » Dom Mar 25, 2018 22:33
João queria um vídeo game que custava R$390,00 e pediu a seus familiares que no Natal, ao invés de presentes, lhe dessem dinheiro. Ganhou de seus avós uma certa quantia, de sua madrinha ganhou a metade dessa quantia, de sua tia ganhou o dobro da quantia que ganhou de seus avós e dos seus pais ganhou o triplo do que ganhou de seus avós, conseguindo assim o valor exato para comprar o vídeo game. Quanto ele ganhou de seus pais?
Olá por favor preciso de ajuda para saber resolver este probleminha e me desculpe se eu estiver no tópico errado por favor me ajudem, eu cheguei até um ponto e não consegui dar a sequencia tipo:
x+x/2+2x+3x=390 preciso saber como continuar por favor me ajudem como faço para chegar no valor de x, muito obrigado por enquanto.
Josemar.
-
Josemar
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sáb Fev 24, 2018 18:53
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Gebe » Dom Mar 25, 2018 22:45
por Gebe » Dom Mar 25, 2018 22:45
Ok, tu fez a parte mais importante da questão, daqui pra frente so precisa tirar o MMC no lado esquerdo e isolar o "x":



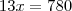

Agora como queremos o valor dado pelos pais, que foi 3x, fazemos:
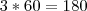
, ou seja, ganhou R$180,00 dos pais
Espero ter ajudado, bons estudos.
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por Josemar » Seg Mar 26, 2018 12:17
por Josemar » Seg Mar 26, 2018 12:17
Olá, muito obrigado , Deus te ilumine e te proteja sempre

-
Josemar
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sáb Fev 24, 2018 18:53
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7721 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13221 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13020 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6091 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8708 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





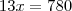

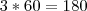 , ou seja, ganhou R$180,00 dos pais
, ou seja, ganhou R$180,00 dos pais



 , avisa que eu resolvo.
, avisa que eu resolvo.

