Olá
Macedo, seja bem-vindo!
macedo1967 escreveu:Determinada quantidade de suco será servida em copos.
Se forem colocados 300 mL em cada copo, serão servidos n copos, e todo o suco será servido;
mas se forem colocados 250 mL em cada copo, será possível servir 4 copos a mais e todo o suco também será servido.
A quantidade de suco, em litros, a ser servida é
(A) 6,5.
(B) 6,0.
(C) 5,5.
(D) 5,0.
(E) 4,5.
Seja

a quantidade de copos e

a quantidade total de suco (em ml). Assim, temos:
Condição I:
macedo1967 escreveu:Se forem colocados 300 mL em cada copo, serão servidos n copos, e todo o suco será servido;...
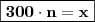 Condição II
Condição II:
macedo1967 escreveu:...mas se forem colocados 250 mL em cada copo, será possível servir 4 copos a mais e todo o suco também será servido.

Para concluir o exercício basta você resolver o sistema formado pelas duas equações acima. Ou seja, determine o valor de "x".
Feito isto, deve encontrar
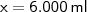
. Que, na verdade, corresponde à SEIS litros.
Espero ter ajudado!
Qualquer dúvida, comente!
Att,
Daniel Ferreira.


 a quantidade de copos e
a quantidade de copos e  a quantidade total de suco (em ml). Assim, temos:
a quantidade total de suco (em ml). Assim, temos: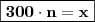

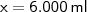 . Que, na verdade, corresponde à SEIS litros.
. Que, na verdade, corresponde à SEIS litros.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)