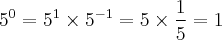por danielneiva » Ter Ago 16, 2016 22:41
por danielneiva » Ter Ago 16, 2016 22:41
O que significa isso que está sublinhado? (Para todo

, tem-se

)
"

" não seria a base da equação? Se

, por que no exemplo logo abaixo

vale 5?

-
danielneiva
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Ago 16, 2016 22:11
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Daniel Bosi » Qua Ago 17, 2016 13:00
por Daniel Bosi » Qua Ago 17, 2016 13:00
Olá danielneiva.
Perceba que qualquer número elevado na zero é igual a 1 (com exceção de zero elevado na zero, que em geral é uma indeterminação).
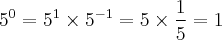
Lembre que todo número elevado na -1 é igual ao seu inverso multiplicativo.
Qualquer dúvida volte a questionar.
-
Daniel Bosi
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Mai 16, 2016 21:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como se aplica a definição de logaritmos nesse calculo:
por andersontricordiano » Qui Abr 07, 2011 16:37
- 1 Respostas
- 1651 Exibições
- Última mensagem por Elcioschin

Qui Abr 07, 2011 18:53
Logaritmos
-
- Como resolver limite exponencial
por joaofonseca » Sex Mar 30, 2012 12:59
- 2 Respostas
- 2226 Exibições
- Última mensagem por joaofonseca

Sáb Mar 31, 2012 11:15
Cálculo: Limites, Derivadas e Integrais
-
- Exponencial de número complexo. Como saio dessa?
por andrina » Sex Nov 19, 2010 15:16
- 1 Respostas
- 2234 Exibições
- Última mensagem por luispereira

Sex Dez 24, 2010 13:24
Números Complexos
-
- [Função exponencial] Não entendi como chegou a formula
por Leti Moura » Ter Jun 12, 2012 21:16
- 2 Respostas
- 4090 Exibições
- Última mensagem por Russman

Qua Jun 13, 2012 00:57
Funções
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13221 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , tem-se
, tem-se  )
) " não seria a base da equação? Se
" não seria a base da equação? Se  , por que no exemplo logo abaixo
, por que no exemplo logo abaixo  vale 5?
vale 5?

 , tem-se
, tem-se  )
) " não seria a base da equação? Se
" não seria a base da equação? Se  , por que no exemplo logo abaixo
, por que no exemplo logo abaixo  vale 5?
vale 5?