A pergunta é a seguinte:
Determinar uma representação paramétrica da reta representada por:
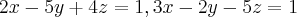
Eu entendi que essas são equações de dois planos, com os vetores normais(n1 e n2) como eles não são combinação um do outro, então, há uma intersecção entre eles, que delimitada por uma reta. Que seria essa reta que pede a representação paramétrica.
Como para representar parametricamente uma reta preciso de um ponto pertencente a ela e o vetor diretor, procurei no Youtube como conseguir os mesmos e me ensinaram assim:
Adotar X=0 para ambas, resolve o sistema com restante, encontrando assim X=0, Y= -3/11 e Z=-1/11, sendo um ponto em comum que atende as duas equações, tendo então o ponto A=(0;-3/11;-1/11). Depois para encontrar um vetor ortogonal simultaneamente aos dois planos( vetor diretor da reta), fazia-se o produto Vetorial dos vetores normais aos planos, obtive o vetor V=3i+2j+1k. Com essas informações, tentei a representação paramétrica, mas o resultado não é igual ao do Livro. Creio ter errado algo ou não ser esse a maneira correta de responder essa questão ou livro está com algum erro. Por isso peço a ajuda de vocês.
Desde já agradeço.
"Felizes aqueles que se divertem com problemas que educam a alma e elevam o espírito." (Fenelon)
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.