![E=t^2-13t+320 \;\;\;\;\;[1] E=t^2-13t+320 \;\;\;\;\;[1]](/latexrender/pictures/67da4b78e7ef767e35bd491b604a0ff9.png)
Buscamos encontrar os valores para t onde o consumo de energia seja no máximo 280 kWh. Assim,
280=t^2-13t+320 \Leftrightarrow t^2-13t + 40 = 0[/tex]
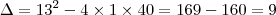
Logo,

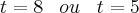
Obtido os valores para t que produzem um gasto de 280 kWh, precisamos saber o intervalo onde este gasto é menor que 280kWh. Assim, colcoando-se estes valores em uma reta, tomaremos um valor à esquerda e um à direita de cada um destes valores, substituindo-se na equação [1] para sabermos se o valor resultante é menor ou maior que 280kWh. Estamos interessados somente nos valores menores que 280 kWh.
-------------------- 5 ------------------- 8 -----------------------------
Tomando t = 4 teremos:
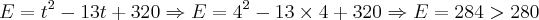
Tomando agora t = 6, teremos:

Tomando-se finalmente t = 9 teremos:
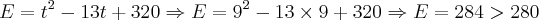
Portanto, os meses cujo gasto é inferior a 280 kWh seriam entre 5 e 8. Ou seja:

b) Obtenha o conjunto solução da equação a seguir.
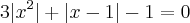
Sabemos que quaisquer valores elevados ao quadrado são positivos e assim, vamos retirá-lo do módulo:

e por definição:
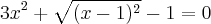
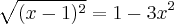
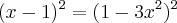



ou, por tentantiva e erro,
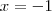
Dividindo-se

por (x + 1) obtemos:

Resolvendo esta equação acima, encontramos os outros valores:
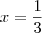
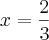
Assim, os valores procurados são:
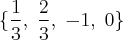
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali


![E=t^2-13t+320 \;\;\;\;\;[1] E=t^2-13t+320 \;\;\;\;\;[1]](/latexrender/pictures/67da4b78e7ef767e35bd491b604a0ff9.png)
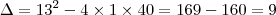

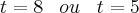
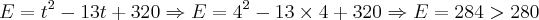

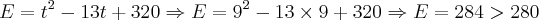

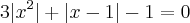

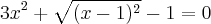
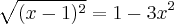
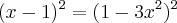



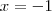

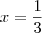
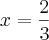
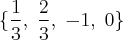

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.