Não há uma solução fácil de ser calculada. Pela aproximação de Newton, obtemos (análise Numérica):
n ##### xn #################### f(xn) #################### f'(xn) #################### x(n+1)
1 ##### 5,000000000 ########## 2,236067977 ########## 10,2236068 ########## 4,781283844
2 ##### 4,781283844 ########## 0,047289898 ########## 9,791231659 ########## 4,776454023
3 ##### 4,776454023 ########## 2,30481E-05 ########## 9,781687597 ########## 4,776451667
4 ##### 4,776451667 ########## 5,48539E-12 ########## 9,781682941 ########## 4,776451667
5 ##### 4,776451667 ########## 0000000000 ########## 9,781682941 ########## 4,776451667
x = 4,776451667
Utilizado:
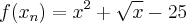
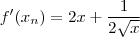
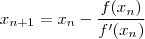
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
![{x}^{2} + \sqrt[]{x} - 25 = 0 {x}^{2} + \sqrt[]{x} - 25 = 0](/latexrender/pictures/c9f3b898c1be36d626990445eb50831c.png)


![{x}^{2} + \sqrt[]{x} - 25 = 0 {x}^{2} + \sqrt[]{x} - 25 = 0](/latexrender/pictures/c9f3b898c1be36d626990445eb50831c.png)

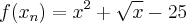
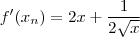
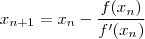



 , avisa que eu resolvo.
, avisa que eu resolvo.

