Bom dia pessoal!
Sou novo aqui no fórum, por isso ainda estou meio perdido. Primeiramente me desculpem se houver algum equivoco na postagem.
Pois bem, tenho a seguinte questão de indução matemática para resolver, consegui chegar tranquilo até o terceiro passo. Lá tem uma parte, inclusive
eu até destaquei no anexo. Eu venho pedir a ajuda de vocês para que possam analisar meu feito e fazer a devida correção se caso precisar.
Obrigado pela atenção de todos.




 .
. ) a afirmação é verdadeira para
) a afirmação é verdadeira para 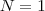 . De fato,
. De fato,
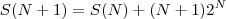
 . Assim,
. Assim, 

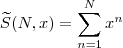 e
e  .
.

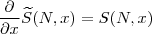 .
. , (não nos preocupemos com o caso x=1), então
, (não nos preocupemos com o caso x=1), então![S(N,x) = \frac{\partial }{\partial x} \frac{x(x^N-1)}{x-1} = \frac{1}{(x-1)^2} [x^N(N(x-1)-1)+1] S(N,x) = \frac{\partial }{\partial x} \frac{x(x^N-1)}{x-1} = \frac{1}{(x-1)^2} [x^N(N(x-1)-1)+1]](/latexrender/pictures/6d4d4a5f31a6b5daa94da51f0ecc3ab6.png)
 temos
temos![S(N,x=2) = \frac{1}{(2-1)^2} [2^N(N(2-1)-1)+1] = 1. [2^N(N.1-1)+1)] = 2^N(N-1) + 1 S(N,x=2) = \frac{1}{(2-1)^2} [2^N(N(2-1)-1)+1] = 1. [2^N(N.1-1)+1)] = 2^N(N-1) + 1](/latexrender/pictures/e4a838575b78fb29334c8c0332adc5bc.png)
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)