Ajuda por favor, na questão abaixo! Grata
Lucas foi passar as férias no Ceará. Lá verificou que, se gastasse R$ 80,00 por dia, poderia permanecer de férias um dia a mais do que se gastasse R$ 90,00. Quanto Lucas possuía?
por mvoporto1986 » Ter Mai 20, 2014 21:35
por Russman » Qua Mai 21, 2014 19:15
. Se ele gastar 
reais por dia de viagem então a quantidade TOTAL de dinheiro que gastará será 
tal que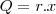
a quantidade de dias da viagem a 80 reais/dia e de 
a quantidade de dias para a viagem de 90 reais/dia. Já que a quantidade de dinheiro que ele possui é fixa, isto é,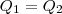 
(índices análogos aos índices de x), então
( equação1)
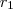e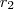 
são conhecidas, são dadas pelo enunciado.mvoporto1986 escreveu:se gastasse R$ 80,00 por dia, poderia permanecer de férias um dia a mais do que se gastasse R$ 90,00.
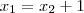(equação2).
. na segunda equação ( bem como está na "equação1") e susbtitua na 1° equação. Fazendo isso você deve calcular 
e 
.
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
zig escreveu:
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.