Olá....
Seja

a fórmula de conversão de Celsius para Fahrenheit.
O primeiro item pede para fazermos duas transformações, ou seja, pede para exibir o valor da temperatura, que está em Fahrenheit, em Celsius. Daí, basta substituirmos na fórmula dada. Observe que trata-se de uma relação tal que substituindo F por valores, obteremos o resultado em Celsius, ou seja, obteremos C. É isto o que queremos. Então:
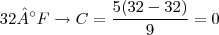
;

;
Bem, o segundo item não ficou muito claro o que está sendo pedido, mas acho que devemos reescrever a equação dada de tal forma que F seja escrita em função de C, ou seja, ao invés de escrever C em função de F, como inicialmente, escreveremos F em função de C. Assim:

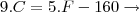
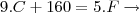
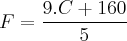
Logo, o que parece que o exercício está pedindo é:
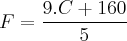
.
Agora, vejamos o último item. Observe que este pede para fazermos a transformação de uma temperatura em Celsius para Fahrenheit. Assim, note que basta aplicarmos a equação encontrada no item anterior. Daí:

;
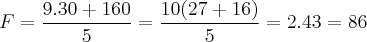
;
Espero ter ajudado....



 a fórmula de conversão de Celsius para Fahrenheit.
a fórmula de conversão de Celsius para Fahrenheit.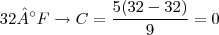 ;
; ;
;
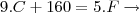
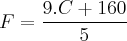
 ;
;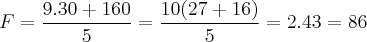 ;
;

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.