 por Cherry » Ter Set 24, 2013 13:21
por Cherry » Ter Set 24, 2013 13:21
1°) Dada a expressão x-2*(3-2x) , qual deve ser o valor de x para que essa expressão seja igual a zero?
2° Sendo A= x/2+2/5 e B=1- -3x/4 ,qual deve ser o valor de x para que se tenha A= B?
3° Um número decimal é tal que 3(1,4-x)+5x= -(x-4,8). Qual é o número x?
Com cálculo.
-
Cherry
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Set 24, 2013 13:11
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por replay » Qua Set 25, 2013 13:22
por replay » Qua Set 25, 2013 13:22
1°)
Eu pensaria da seguinte forma, qual valor eu coloco para dar um valor zero?
Se você colocar x = 2, a questão vai dar zero, pois qualquer numero multiplicado por zero é zero.
O Enunciado está certo mesmo ou é (x-2)(3-2x) ????
Se for (x-2)(3-2x) admite duas respostas:
ou x-2=0
x=2
ou
3-2x=0
2x=3
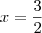
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- calculos
por flavio970 » Sex Out 16, 2015 12:40
- 1 Respostas
- 3027 Exibições
- Última mensagem por nakagumahissao

Sex Nov 06, 2015 10:58
Números Complexos
-
- [Site de Calculos]calculafacil.com.br
por calculafacil » Ter Set 13, 2011 01:43
- 5 Respostas
- 4887 Exibições
- Última mensagem por Neperiano

Seg Out 10, 2011 16:59
Assuntos Gerais ou OFF-TOPIC
-
- [CÁLCULOS] LINHA DE MONTAGEM
por diclas » Ter Jun 05, 2012 11:56
- 1 Respostas
- 1893 Exibições
- Última mensagem por Neperiano

Qua Out 24, 2012 14:48
Sequências
-
- [Matrizes] Site de cálculos matriciais
por Gustavo Lee » Ter Jul 17, 2012 19:44
- 2 Respostas
- 5200 Exibições
- Última mensagem por e8group

Qua Jul 18, 2012 10:23
Sites Recomendados / Outras Indicações
-
- me ajudem calculos para antecipar parcelas
por MABafi » Dom Jul 18, 2010 23:36
- 0 Respostas
- 1603 Exibições
- Última mensagem por MABafi

Dom Jul 18, 2010 23:36
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.