A quantia de R$ 2.000,00 vai ser dividida igualmente entre x
pessoas. Como faltaram 5 pessoas, cada uma das restantes
recebeu R$ 20,00 a mais. Determine o número de pessoas que
participaram.
a) 25.
b) 30.
c) 28.
d) 20.
Resposta: A
Eu tentei chegar a uma solução da seguinte maneira:
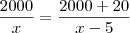
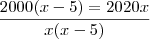
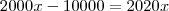



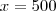
Como você viu, cheguei a um resultado bem diferente, creio que minha solução está errada.
Alguém poderia me ajudar a chegar uma solução correta? agradeço desde ja.



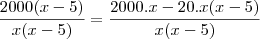
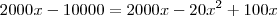
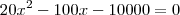




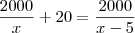
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)