-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478537 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 533586 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 497108 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 710772 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2130390 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Myllena » Dom Dez 02, 2012 02:51
por Myllena » Dom Dez 02, 2012 02:51
Se você traçar a reta que contém os pares ordenados que são soluções de x + y = 2 e a reta que contém os pares ordenados que são soluções de x + y = 4 , em um mesmo gráfico , qual desses pares ordenados será o ponto do cruzamento das duas retas: (3, 1) , (3, -1) , ou (4, 0) ? em seguida construa o gráfico para confirmar sua resposta .
obs : (fiquei o bimestre todo sem nenhum professor só chegou uma diretora lá e falou pra gente fazer um trabalho em vez da prova e eu não estou intendendo NADA !) e eu preciso muito de tirar 100 , me ajuuuuuda !! vou ter infarte ..
Tem que fazer a conta e
-
Myllena
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Dez 02, 2012 02:34
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: Escola
- Andamento: cursando
 por DanielFerreira » Dom Dez 02, 2012 18:24
por DanielFerreira » Dom Dez 02, 2012 18:24
Olá
Myllena,
seja bem-vinda!
Um par ordenado é representador por
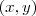
, onde o

recebe o nome de
Abscissa e o

o nome de
ordenada.
O ponto de cruzamento entre as equações é um ponto, certo?! Esse ponto é comum as duas equações, ou seja, o ponto que passa pela equação

passa também por
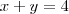
. Enfim, você deverá testar os pontos que foram dados e verificar qual deles é o procurado.
Vou tentar o primeiro ponto e você verifica os outros dois, ok?!

Isso significa que

e

Testando na equação
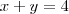
, veja:
x + y = 4
3 + 1 = 4
4 = 4 É VERDADEIRA!!!!
Testando na equação

, veja:
x + y = 2
3 + 1 = 2
4 = 2 É FALSA!!!!
Para que esse ponto fosse a resposta, teria que ser verdadeira nas duas equações, lembre-se disso. Então, podemos concluir que esse ponto não é o que procuramos.
Agora é com você.
Até breve!!
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Pares ordenados !
por LuizCarlos » Sáb Ago 20, 2011 17:35
- 6 Respostas
- 2419 Exibições
- Última mensagem por LuizCarlos

Sáb Ago 20, 2011 23:20
Álgebra Elementar
-
- Função [ pares ordenados ]
por my2009 » Qua Mai 27, 2015 18:03
- 0 Respostas
- 1177 Exibições
- Última mensagem por my2009

Qua Mai 27, 2015 18:03
Funções
-
- Conjuntos/Pares ordenados
por gustavoduflot » Qua Jun 03, 2015 23:09
- 1 Respostas
- 1303 Exibições
- Última mensagem por DanielFerreira

Qui Jun 04, 2015 23:06
Conjuntos
-
- Multiplicação e Adição de Pares Ordenados
por raymondtfr » Sáb Nov 22, 2014 04:17
- 0 Respostas
- 1709 Exibições
- Última mensagem por raymondtfr

Sáb Nov 22, 2014 04:17
Funções
-
- Descobrir pontos da Reta Numérica
 por Duartemaria » Ter Dez 16, 2014 19:10
por Duartemaria » Ter Dez 16, 2014 19:10
- 4 Respostas
- 1874 Exibições
- Última mensagem por adauto martins

Sex Dez 19, 2014 12:46
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


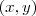 , onde o
, onde o  recebe o nome de
recebe o nome de  o nome de
o nome de  passa também por
passa também por 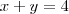 . Enfim, você deverá testar os pontos que foram dados e verificar qual deles é o procurado.
. Enfim, você deverá testar os pontos que foram dados e verificar qual deles é o procurado.
 e
e 






