Se você traçar a reta que contém os pares ordenados que são soluções de x + y = 2 e a reta que contém os pares ordenados que são soluções de x + y = 4 , em um mesmo gráfico , qual desses pares ordenados será o ponto do cruzamento das duas retas: (3, 1) , (3, -1) , ou (4, 0) ? em seguida construa o gráfico para confirmar sua resposta .
obs : (fiquei o bimestre todo sem nenhum professor só chegou uma diretora lá e falou pra gente fazer um trabalho em vez da prova e eu não estou intendendo NADA !) e eu preciso muito de tirar 100 , me ajuuuuuda !! vou ter infarte ..
Tem que fazer a conta e


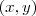 , onde o
, onde o  recebe o nome de
recebe o nome de  o nome de
o nome de  passa também por
passa também por 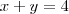 . Enfim, você deverá testar os pontos que foram dados e verificar qual deles é o procurado.
. Enfim, você deverá testar os pontos que foram dados e verificar qual deles é o procurado.
 e
e 
