 , em que c e d são coeficientes reais, então uma outra raiz dessa equação é:
, em que c e d são coeficientes reais, então uma outra raiz dessa equação é:A) 1
B) 2
C) 3
D) 4
E) 5
Sempre tenho duvidas na hora de fazer equações de terceiro grau e essa me pareceu ainda mais complicada.
A resposta é C, como resolvo?

 , em que c e d são coeficientes reais, então uma outra raiz dessa equação é:
, em que c e d são coeficientes reais, então uma outra raiz dessa equação é:
 nesta equação. Depois, lembre-se que o conjugado também é raíz, logo
nesta equação. Depois, lembre-se que o conjugado também é raíz, logo  também satisfaz
também satisfaz 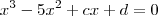 . Substitua e resolva para
. Substitua e resolva para  e
e  .
.

 na equação achei
na equação achei 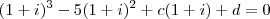
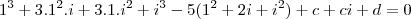
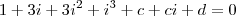
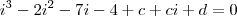
 ? Como resolvo para c e d?
? Como resolvo para c e d?
 . Você terá um sistema com duas equações e duas incógnitas envolvendo
. Você terá um sistema com duas equações e duas incógnitas envolvendo  e
e  , que você resolve como outro sistema qualquer.
, que você resolve como outro sistema qualquer.





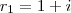 e
e 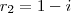 , vamos descobrir
, vamos descobrir 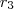
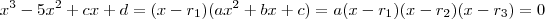
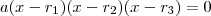 , e reagrupando vamos obbter :
, e reagrupando vamos obbter : 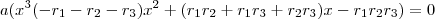
 . lembrando que ,
. lembrando que , 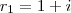 e
e 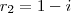 , finalmente segue que ,
, finalmente segue que , 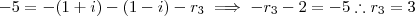 .
. 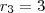



 , definida por
, definida por 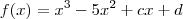 . Sabemos que quando
. Sabemos que quando 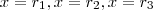 ,
, 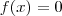 . Além disso , podemos escrever
. Além disso , podemos escrever  como produto de funções . Sejam
como produto de funções . Sejam 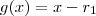 e
e  tal que ,
tal que , 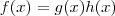 para
para 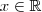 e
e 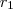 seja raiz de
seja raiz de  e
e 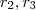 sejam raízes de
sejam raízes de 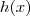 .
. 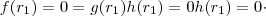 e
e 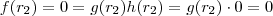 e finalmente
e finalmente 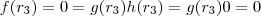 .
. 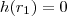 mas como
mas como 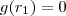 ,orá qualquer número real multiplicado por zero o resultado será zero . Analogamente , concluimos para os outros casos .
,orá qualquer número real multiplicado por zero o resultado será zero . Analogamente , concluimos para os outros casos . 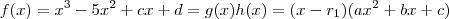 . Para estabelecer esta igualdade , os coeficientes correspondentes das funções polinomiais devem ser iguais . (Por que ?? )
. Para estabelecer esta igualdade , os coeficientes correspondentes das funções polinomiais devem ser iguais . (Por que ?? ) 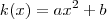 . Agora seja
. Agora seja 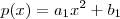 , perceba que
, perceba que 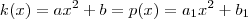 se , e somente
se , e somente 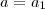 e
e 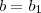 . Este exemplo só foi uma introdução .
. Este exemplo só foi uma introdução .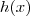 na forma fatorada , isto é
na forma fatorada , isto é  ( Por que ?? )
( Por que ?? ) 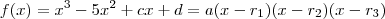
![\implies f(x) = a \left[ (x-r_1)(x^2 - r_3 x - r_2 x + r_ 2r_3) \right ] \implies f(x) = a \left[ (x-r_1)(x^2 - r_3 x - r_2 x + r_ 2r_3) \right ]](/latexrender/pictures/0a87ba4d31f8da5e4870cf6d291e561d.png)
![\implies f(x) = a \left[ (x-r_1)(x^2 + (-r_3 -r_2)x + r_2 r_3) \right ] \implies f(x) = a \left[ (x-r_1)(x^2 + (-r_3 -r_2)x + r_2 r_3) \right ]](/latexrender/pictures/8064348ac1dfc05f4dcc1854ac17153a.png)
![\implies f(x) = a \left[ x^3 + (-r_3 -r_2)x^2 + r_2 r_3 x - r_1 x^2+ (r_3 r_1 + r_2 r_1)x - r_1r_2r_3\right ] \implies f(x) = a \left[ x^3 + (-r_3 -r_2)x^2 + r_2 r_3 x - r_1 x^2+ (r_3 r_1 + r_2 r_1)x - r_1r_2r_3\right ]](/latexrender/pictures/b089b74a212e029e9c10e118f1ca5c0f.png)
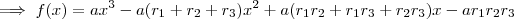
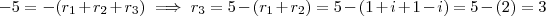


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.