Estou com duvidas em:
Generalize o procedimento de completamento de trinômio quadrado perfeito para os casos:
(a) x^2 + b x + c = 0
(b) ax^2 + b x + c = 0




 , se o mesmo estivesse incompleto como ,
, se o mesmo estivesse incompleto como ,  , poderíamos add um mesmo elemento real nos dois lados da igualdade ou multiplicarmos por uma constante diferente que zero que não estaríamos mudando o resultado . De forma similar , perceba que
, poderíamos add um mesmo elemento real nos dois lados da igualdade ou multiplicarmos por uma constante diferente que zero que não estaríamos mudando o resultado . De forma similar , perceba que 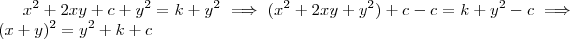 .
.  e reescrever de uma forma compacta ,
e reescrever de uma forma compacta , 

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

