![x^3-3x^2 + [27(2-27) +2]x-27(-25)= 0](/latexrender/pictures/7d01b86c7fd21a6d329ef05662f9363b.png "x^3-3x^2 + [27(2-27) +2]x-27(-25)= 0")
Ao resolver esta equação, cheguei a esse resultado abaixo.
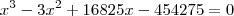
Assim estive pensando em substituir o valor de x por 27, pois esse numero anula esses números maiores, mas não anula o valor de
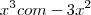.Como faço para encontrar a primeira solução?
por +Danilo2 » Sáb Out 08, 2016 18:11
.
por petras » Seg Dez 12, 2016 11:17
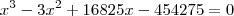
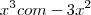![{x}^{3}-3{x}^{2}+\left[(27.-25)+2) \right]x-27(-25) = 0\\
{x}^{3}-3{x}^{2}-673x+675= 0](/latexrender/pictures/d2c5d5038bb9e65ec0d42d3fa5b9f84a.png "{x}^{3}-3{x}^{2}+\left[(27.-25)+2) \right]x-27(-25) = 0\\
{x}^{3}-3{x}^{2}-673x+675= 0")
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)