 por Debylow » Qua Nov 14, 2012 16:07
por Debylow » Qua Nov 14, 2012 16:07
Não sei por que tenho essa maldita dúvida , as vezes eu faço certo , mas é na sorte , e eu queria acabar com ela de uma vez por todas . É muito boba , é sobre uma equação do 1° grau , lá vai:
quando tem isso:

não sei se o
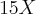
vai na frente ou atrás do
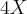
.
Outro exemplo:

, nesse caso nao sei se o

vai na frente ou atrás do

. Olha como ficaria a minha:
9X+3=2X
9X-2X=-3
7X=-3
X=
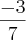
e a primeira:
4X-4=15X+3
nessa eu coloco o 15X na frente do 4X , sendo que na outra eu coloquei o n° que passava , atrás , errado?
15X-4X=3+4
11X=7

Por favor me tirem essa dúvida
-
Debylow
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Nov 13, 2012 17:37
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por Cleyson007 » Qua Nov 14, 2012 16:21
por Cleyson007 » Qua Nov 14, 2012 16:21
Olá boa tarde!
Tanto faz o 15x ir para frente ou para trás.. A questão é "isolar" os elementos que tem x de um lado e os que não tem do outro lado. Acompanhe:
4x - 15x = 3 + 4 (Joguei os elementos com x para a esquerda e os sem x para a direita --> repare que quando passo para o outro lado da igualdade mudo o sinal).
Ou, 15x - 4x = - 4 -3
Resolvendo, 11x = -7 --> x = -7/11
O seu segundo exemplo está resolvido corretamente!
Comente qualquer dúvida

Att,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Debylow » Qua Nov 14, 2012 17:24
por Debylow » Qua Nov 14, 2012 17:24
tirei minha dúvida , obg. mas se eu posso colocar em qualquer sequencia :4x-15x=3+4 , nessa o resultado daria 7/11, e se eu colocasse 4x-15x=-3-4 daria -7/11 , pq?
-
Debylow
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Nov 13, 2012 17:37
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por MarceloFantini » Qua Nov 14, 2012 19:38
por MarceloFantini » Qua Nov 14, 2012 19:38
A ordem é importante pelo seguinte aspecto: quando você tem uma certa igualdade, somar ou subtrair um número de ambos lados mantém a igualdade. Por exemplo,

e também

ou

.
Este processo que alguns chamam de "passar para um lado" na verdade consiste em somar a mesma quantidade de ambos lados, mas tendo em mente o seguinte fato: um número menos ele mesmo é zero.
Logo, na primeira equação que mostrou temos
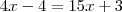
. Somando
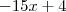
dos dois lados segue

, que resulta em

e portanto
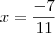
.
Você poderia ter decidido somar

para anular
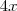
à esquerda e

à direita e chegaria na mesma resposta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jefferson0209 » Ter Set 22, 2015 15:26
por jefferson0209 » Ter Set 22, 2015 15:26
preciso de uma ajuda,ñ consigo resolver um calculo de logaritimo
log (x-9)=2 me ajudem
. 6
-
jefferson0209
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Ter Set 22, 2015 15:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: matematica
- Andamento: cursando
 por jefferson0209 » Ter Set 22, 2015 17:18
por jefferson0209 » Ter Set 22, 2015 17:18
alguem me ajuda ae?
1)sendo log2=u e log3=v,determine:
a)log12
b)log15
2)calcula:
log 81+ log625-log100
.. 3 . . 5
-
jefferson0209
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Ter Set 22, 2015 15:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: matematica
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida boba!
por zenildo » Dom Dez 21, 2014 00:48
- 2 Respostas
- 1838 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:23
Trigonometria
-
- Dúvida boba!
por zenildo » Ter Jan 13, 2015 01:17
- 11 Respostas
- 10854 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:24
Números Complexos
-
- Divisao de polinômios.. duvida boba?
por vinik1 » Qui Mar 31, 2011 23:25
- 4 Respostas
- 3405 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:31
Polinômios
-
- Duvida equação do 1 grau
por tadeutato » Qua Abr 27, 2011 14:24
- 1 Respostas
- 1432 Exibições
- Última mensagem por Neperiano

Qua Abr 27, 2011 14:29
Cálculo: Limites, Derivadas e Integrais
-
- Equação de 2º grau - Dúvida
por Brenitchow » Qua Jun 20, 2012 17:25
- 1 Respostas
- 1463 Exibições
- Última mensagem por MarceloFantini

Qua Jun 20, 2012 20:47
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

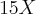 vai na frente ou atrás do
vai na frente ou atrás do 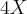 .
. , nesse caso nao sei se o
, nesse caso nao sei se o  vai na frente ou atrás do
vai na frente ou atrás do  . Olha como ficaria a minha:
. Olha como ficaria a minha: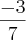






 e também
e também  ou
ou  .
.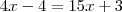 . Somando
. Somando 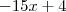 dos dois lados segue
dos dois lados segue  , que resulta em
, que resulta em  e portanto
e portanto 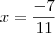 .
. para anular
para anular 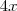 à esquerda e
à esquerda e  à direita e chegaria na mesma resposta.
à direita e chegaria na mesma resposta.



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.