karenblond,
Muito bem! Ví que sabe fatorar corretamente. E já fez a parte mais difícil do problema! Vou colocar a equação abaixo:
![\frac{2x + 1}{x - 3} + \frac{2}{x^2 - 9} = 1 \;\;\;\;\;\; [1] \frac{2x + 1}{x - 3} + \frac{2}{x^2 - 9} = 1 \;\;\;\;\;\; [1]](/latexrender/pictures/c953fb41681e6bdd48ffce7ed2bd6758.png)
Apesar de ter feito corretamente a fatoração da segunda fração, houve um erro ao continuar o processo. Tente fazer da seguinte forma: Primeiramente Deixe o MMC colocado num canto da folha e olhe para o problema [1] novamente. Você vai precisar pegar o MMC obtido, dividir por cada um dos denominadores e multiplicar por cada um dos numeradores colocando tudo sobre uma só fração:
Reescrevendo a fração ficará:
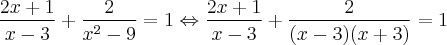
Na primeira fração temos (x - 3) e na segunda, agora temos (x - 3)(x+3). Assim, o MMC será:

Dividindo-se esse MMC pelo denominador da primeira fração teremos:
![MMC = (x -3)(x+3) \Rightarrow \frac{(x -3)(x+3)}{(x -3)} = x + 3 \;\;\;\;\;\; [2] MMC = (x -3)(x+3) \Rightarrow \frac{(x -3)(x+3)}{(x -3)} = x + 3 \;\;\;\;\;\; [2]](/latexrender/pictures/1bc910e5ff2b656cf0a689c1d4069ae0.png)
Tudo bem até aqui? Olhando para esta divisão seria a mesma coisa se pegássemos um número qualquer, por exemplo 4 x 3 e dividíssemos por 4 e daria o 3; Ou ainda, como outro exemplo:

Muito bem, agora que temos o resultado da divisão do MMC pelo primeiro denominador, temos ainda que multiplicar pelo numerador daquela fração, que é 2x + 1! Recapitulado:
![MMC = (x -3)(x+3) \Rightarrow \frac{(x -3)(x+3)}{(x -3)} = x + 3 \;\;\;\;\;\; [2] MMC = (x -3)(x+3) \Rightarrow \frac{(x -3)(x+3)}{(x -3)} = x + 3 \;\;\;\;\;\; [2]](/latexrender/pictures/1bc910e5ff2b656cf0a689c1d4069ae0.png)
Pegando-se este resultado da divisão mostrado em [2] acima, ou seja, (x + 3), temos que multiplicá-lo pelo numerador (2x + 1). Fazendo esta multiplicação à parte, teremos:
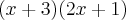
Lembro que a multiplicação de expressões como essa funciona da seguinte forma. "Temos duas expressões: (x + 3) e (2x + 1); Pega-se o x da primeira expressão e multiplica-se pelo primeiro e pelo segundos termos da segunda expressão, respeitando-se os sinais e soma-se com o segundo termo da primeira multiplicado pelos primeiro e segundo termo da segunda expressao - Simplicando: O primeiro vezes o primeiro e o segundo mais o segundo vezes o primeiro e o segundo de novo".
Assim, +x vezes +2x mais +x vezes +1 mais +3 vezes +2x mais +3 vezes +1 que ficará da seguinte forma:
![(x + 3) (2x + 1) = \left[(+x) \times (+2x) + (+x) \times (+1) + (+3) \times (+2x) + (+3) \times (+1) \right] (x + 3) (2x + 1) = \left[(+x) \times (+2x) + (+x) \times (+1) + (+3) \times (+2x) + (+3) \times (+1) \right]](/latexrender/pictures/d7955bf68b400e7eb7e1c4fc0a17dbb2.png)
que dará:
![= 2x^{2} + x + 6x + 3 = 2x^2 + 7x + 3 \;\;\;\;\;\; [3] = 2x^{2} + x + 6x + 3 = 2x^2 + 7x + 3 \;\;\;\;\;\; [3]](/latexrender/pictures/b98f7e4cc57319b8807261c912e4df23.png)
Vou colocar agora esse resultado sobre a fração final. O MMC fica no denominador e o resultado [3] no numerador. Os pontinhos que deixei estão aí porque ainda não terminamos a conta ainda:
![\frac{2x + 1}{x - 3} + \frac{2}{x^2 - 9} = 1 \Leftrightarrow \frac{2x^2 + 7x + 3 \cdot \cdot \cdot }{(x - 3)(x + 3)} = 1 \;\;\;\; [4] \frac{2x + 1}{x - 3} + \frac{2}{x^2 - 9} = 1 \Leftrightarrow \frac{2x^2 + 7x + 3 \cdot \cdot \cdot }{(x - 3)(x + 3)} = 1 \;\;\;\; [4]](/latexrender/pictures/f0d25e18162268ca6ba0c093df3a654d.png)
Agora terminamos as operações necessárias com o MMC na primeira fração. Precisamos fazer o mesmo para a segunda. Essa será bem mais fácil porque:
![\frac{(x - 3)(x + 3)}{(x - 3)(x + 3)} = 1 \;\;\;\;\; [5] \frac{(x - 3)(x + 3)}{(x - 3)(x + 3)} = 1 \;\;\;\;\; [5]](/latexrender/pictures/4cf90534368418bfdebd07c4117d2b42.png)
Isto ocorre para qualquer valor de x tal que:

Se x fosse igual a 3 ou -3, o denominador ficaria - Para x = 3 => (x - 3)(x + 3) = (3 -3)(3 + 3) = 0 x 6 = 0 e para x = -3 ficaria (x - 3)(x + 3) = (-3 -3)(-3 + 3) = (-6) x 0 = 0 e sabemos que o denominador "Nunca" poderá ser zero porque causaria uma INDETERMINAÇÃO, por isso é importante frisar que

apesar de que no seu problema não será utilizado.
Agora que já sabemos que, para a SEGUNDA fração, divindo-se o MMC por (x - 3)(x+3) dá 1 (Veja [5]), agora só falta multiplicar esse "1" pelo numerador que na SEGUNDA fração é 2. Assim, 1 x 2 = 2 e assim substituir os três pontinhos que deixamos na expressão [4] acima da seguinte maneira:

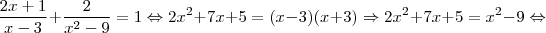

Assim terminamos de trabalhar com estas frações. Aviso-lhe que a equação:

não possui solução Real (Conjunto dos números Reais). Há apenas solução no conjunto dos Números Complexos, por isso, deixarei como está.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali










![\frac{2x + 1}{x - 3} + \frac{2}{x^2 - 9} = 1 \;\;\;\;\;\; [1] \frac{2x + 1}{x - 3} + \frac{2}{x^2 - 9} = 1 \;\;\;\;\;\; [1]](/latexrender/pictures/c953fb41681e6bdd48ffce7ed2bd6758.png)
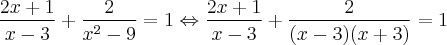

![MMC = (x -3)(x+3) \Rightarrow \frac{(x -3)(x+3)}{(x -3)} = x + 3 \;\;\;\;\;\; [2] MMC = (x -3)(x+3) \Rightarrow \frac{(x -3)(x+3)}{(x -3)} = x + 3 \;\;\;\;\;\; [2]](/latexrender/pictures/1bc910e5ff2b656cf0a689c1d4069ae0.png)

![MMC = (x -3)(x+3) \Rightarrow \frac{(x -3)(x+3)}{(x -3)} = x + 3 \;\;\;\;\;\; [2] MMC = (x -3)(x+3) \Rightarrow \frac{(x -3)(x+3)}{(x -3)} = x + 3 \;\;\;\;\;\; [2]](/latexrender/pictures/1bc910e5ff2b656cf0a689c1d4069ae0.png)
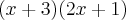
![(x + 3) (2x + 1) = \left[(+x) \times (+2x) + (+x) \times (+1) + (+3) \times (+2x) + (+3) \times (+1) \right] (x + 3) (2x + 1) = \left[(+x) \times (+2x) + (+x) \times (+1) + (+3) \times (+2x) + (+3) \times (+1) \right]](/latexrender/pictures/d7955bf68b400e7eb7e1c4fc0a17dbb2.png)
![= 2x^{2} + x + 6x + 3 = 2x^2 + 7x + 3 \;\;\;\;\;\; [3] = 2x^{2} + x + 6x + 3 = 2x^2 + 7x + 3 \;\;\;\;\;\; [3]](/latexrender/pictures/b98f7e4cc57319b8807261c912e4df23.png)
![\frac{2x + 1}{x - 3} + \frac{2}{x^2 - 9} = 1 \Leftrightarrow \frac{2x^2 + 7x + 3 \cdot \cdot \cdot }{(x - 3)(x + 3)} = 1 \;\;\;\; [4] \frac{2x + 1}{x - 3} + \frac{2}{x^2 - 9} = 1 \Leftrightarrow \frac{2x^2 + 7x + 3 \cdot \cdot \cdot }{(x - 3)(x + 3)} = 1 \;\;\;\; [4]](/latexrender/pictures/f0d25e18162268ca6ba0c093df3a654d.png)
![\frac{(x - 3)(x + 3)}{(x - 3)(x + 3)} = 1 \;\;\;\;\; [5] \frac{(x - 3)(x + 3)}{(x - 3)(x + 3)} = 1 \;\;\;\;\; [5]](/latexrender/pictures/4cf90534368418bfdebd07c4117d2b42.png)



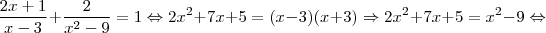



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.