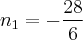Sabe-se que o número de andares é igual ao triplo do número de aptos. mais 2. Isto quer dizer que:
Seja n o número de apartamentos e a o número de andares. Tem-se que:
a = 3n + 2
Tomando-se t como sendo o total de apartamentos e considerando que o total de aptos. nesse prédio é 56, tem-se:
t = 56 = a * n = (3n + 2).n =

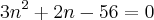
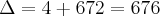
![n = \frac{-2 \pm \sqrt[]{\Delta}}{6} = \frac{-2 \pm 26}{6} n = \frac{-2 \pm \sqrt[]{\Delta}}{6} = \frac{-2 \pm 26}{6}](/latexrender/pictures/a1be7f6126d5666c29da58232e0c7f27.png)
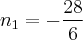

Como números negativos não nos interessam, n assume o valor de 4.
Logo, de a = 3n + 2 => a = 12 + 2 = 14
O Número de Andares é portanto 14 e o número de apartamentos por andar é 4, que é a quantidade procurada.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali




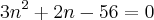
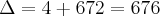
![n = \frac{-2 \pm \sqrt[]{\Delta}}{6} = \frac{-2 \pm 26}{6} n = \frac{-2 \pm \sqrt[]{\Delta}}{6} = \frac{-2 \pm 26}{6}](/latexrender/pictures/a1be7f6126d5666c29da58232e0c7f27.png)