 por Sobreira » Dom Fev 23, 2014 18:48
por Sobreira » Dom Fev 23, 2014 18:48
Boa tarde.
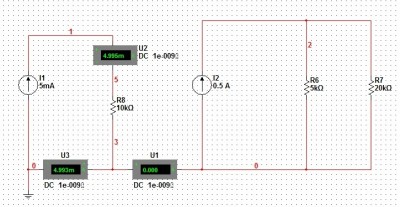
Estava resolvendo um exercício a respeito do circuito abaixo e me deparei com uma dúvida:
Eu entendo que a corrente no nó 3, abaixo do resistor de 10Kohms se divide entre voltar para a fonte de 5 mA e para o outro lado (direito) do circuito. Mas aí que está:
Como ela se comporta lá?? Ela sobe pelos três ramos ??? Mas e depois, ela não deveria voltar para a fonte de 5mA ???
Simulando este circuito, o amperímetro U1 indica que não há corrente neste trecho, mostrando que na realidade temos duas malhas completamente independentes.
Não deveria haver corrente naquele ramo???
- Anexos
-
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por young_jedi » Dom Fev 23, 2014 19:01
por young_jedi » Dom Fev 23, 2014 19:01
nesse caso é como se você tivesse duas malhas isoladas, a corrente sempre tem que ter um caminho de retorno
neste casso como só temos uma conexão entre as duas malhas não tem como a corrente circular entre as duas, portanto não existe corrente circulando por aquele ramo
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Sobreira » Dom Fev 23, 2014 21:39
por Sobreira » Dom Fev 23, 2014 21:39
Quer dizer então que é como se a corrente não pode ir e voltar por este mesmo ramo ??? Ela teria que ir para o lado direito por um ramo e retornar por outro ???
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por young_jedi » Dom Fev 23, 2014 22:34
por young_jedi » Dom Fev 23, 2014 22:34
isso exatamente, teria que haver dois caminhos um de ida e outro de retorno para a corrente
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Espaço vetorial - Vetor nulo
por Razoli » Qua Mar 18, 2015 19:03
- 0 Respostas
- 1155 Exibições
- Última mensagem por Razoli

Qua Mar 18, 2015 19:03
Álgebra Linear
-
- Circuito Elétrico
 por Rafael16 » Seg Mar 18, 2013 19:19
por Rafael16 » Seg Mar 18, 2013 19:19
- 1 Respostas
- 11760 Exibições
- Última mensagem por young_jedi

Seg Mar 18, 2013 20:43
Eletricidade I
-
- Circuito Elétrico sem solução.
 por Sobreira » Qui Set 19, 2013 02:20
por Sobreira » Qui Set 19, 2013 02:20
- 3 Respostas
- 7928 Exibições
- Última mensagem por young_jedi

Sáb Set 21, 2013 11:27
Aritmética
-
- Dúvida circuito magnético.
 por Sobreira » Sáb Mar 14, 2015 19:57
por Sobreira » Sáb Mar 14, 2015 19:57
- 0 Respostas
- 1812 Exibições
- Última mensagem por Sobreira

Sáb Mar 14, 2015 19:57
Cálculo: Limites, Derivadas e Integrais
-
- Calculo circuito - Resistores
 por Vencill » Dom Abr 26, 2015 19:46
por Vencill » Dom Abr 26, 2015 19:46
- 0 Respostas
- 6331 Exibições
- Última mensagem por Vencill

Dom Abr 26, 2015 19:46
Eletricidade I
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
