 por silviopuc » Dom Dez 01, 2013 16:42
por silviopuc » Dom Dez 01, 2013 16:42
Não consegui chegar no gabarito. Alguém poderia ajudar, por favor!
Se
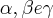
são raízes da equação
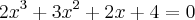
, então
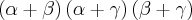
é igual a:
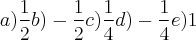
Gabarito: A
-
silviopuc
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Jan 15, 2013 12:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Dom Dez 01, 2013 18:43
por e8group » Dom Dez 01, 2013 18:43
Só por simplicidade vamos trocar alpha ,beta ,gamma respect. por a,b,c .
Expandindo

teremos

(1) (muito obrigado Wolfram alpha ! ) ,agorá é só "brincar" com os a,b,c de modo a usar as
Relações de Girard que estabelece uma relação entre as raízes de um polinômio e os seus coeficientes . De acordo com estas relações ,dada equação polinomial
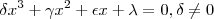
cuja raízes reais são

,temos os resultados :
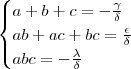
.
Seja
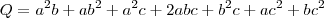
, segue
![Q = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(bc) ] + [c(ab) + c(ac) + c(cb)] Q = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(bc) ] + [c(ab) + c(ac) + c(cb)]](/latexrender/pictures/f7b1996e7a71532fe87986ec2566c5e4.png)
e add
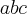
nos dois lados da igualdade
![Q +abc = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(ac)+ b(bc) ] + [c(ab) + c(ac) + c(cb)] Q +abc = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(ac)+ b(bc) ] + [c(ab) + c(ac) + c(cb)]](/latexrender/pictures/44f06630283829a20ee3f2a62ce46c6d.png)
e assim obtemos

e portanto
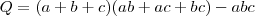
Se não errei contas é isso . Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por silviopuc » Ter Dez 03, 2013 00:06
por silviopuc » Ter Dez 03, 2013 00:06
Muito obrigado!
santhiago escreveu:Só por simplicidade vamos trocar alpha ,beta ,gamma respect. por a,b,c .
Expandindo

teremos

(1) (muito obrigado Wolfram alpha ! ) ,agorá é só "brincar" com os a,b,c de modo a usar as
Relações de Girard que estabelece uma relação entre as raízes de um polinômio e os seus coeficientes . De acordo com estas relações ,dada equação polinomial
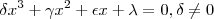
cuja raízes reais são

,temos os resultados :
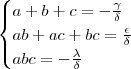
.
Seja
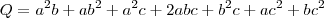
, segue
![Q = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(bc) ] + [c(ab) + c(ac) + c(cb)] Q = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(bc) ] + [c(ab) + c(ac) + c(cb)]](/latexrender/pictures/f7b1996e7a71532fe87986ec2566c5e4.png)
e add
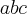
nos dois lados da igualdade
![Q +abc = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(ac)+ b(bc) ] + [c(ab) + c(ac) + c(cb)] Q +abc = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(ac)+ b(bc) ] + [c(ab) + c(ac) + c(cb)]](/latexrender/pictures/44f06630283829a20ee3f2a62ce46c6d.png)
e assim obtemos

e portanto
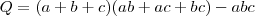
Se não errei contas é isso . Tente concluir .
-
silviopuc
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Jan 15, 2013 12:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Resolução de equações
por anfalop » Qui Mai 31, 2012 22:44
- 1 Respostas
- 1239 Exibições
- Última mensagem por Russman

Qui Mai 31, 2012 23:08
Sistemas de Equações
-
- [Resolução de equações polinomiais]
por ZANGARO » Qui Fev 27, 2014 21:16
- 1 Respostas
- 1243 Exibições
- Última mensagem por Russman

Sex Fev 28, 2014 14:23
Equações
-
- Resolução de equações com logaritmo
por Ana Saldanha » Sáb Mar 22, 2014 17:23
- 1 Respostas
- 1867 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 22, 2014 19:24
Logaritmos
-
- [sistemas de equaçoes]resoluçao com multiplicaçao
por guillcn » Qui Out 06, 2011 10:51
- 4 Respostas
- 4083 Exibições
- Última mensagem por guillcn

Qua Out 26, 2011 15:28
Sistemas de Equações
-
- Resolução de dois problemas do 2° grau
por guilhermearisio » Dom Mai 22, 2011 16:12
- 2 Respostas
- 3849 Exibições
- Última mensagem por guilhermearisio

Dom Mai 22, 2011 23:19
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
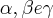 são raízes da equação
são raízes da equação 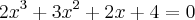 , então
, então 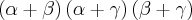 é igual a:
é igual a: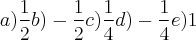

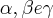 são raízes da equação
são raízes da equação 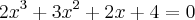 , então
, então 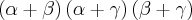 é igual a:
é igual a: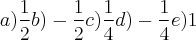

 teremos
teremos  (1) (muito obrigado Wolfram alpha ! ) ,agorá é só "brincar" com os a,b,c de modo a usar as Relações de Girard que estabelece uma relação entre as raízes de um polinômio e os seus coeficientes . De acordo com estas relações ,dada equação polinomial
(1) (muito obrigado Wolfram alpha ! ) ,agorá é só "brincar" com os a,b,c de modo a usar as Relações de Girard que estabelece uma relação entre as raízes de um polinômio e os seus coeficientes . De acordo com estas relações ,dada equação polinomial 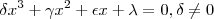 cuja raízes reais são
cuja raízes reais são  ,temos os resultados :
,temos os resultados : 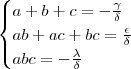 .
. 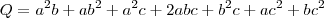 , segue
, segue ![Q = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(bc) ] + [c(ab) + c(ac) + c(cb)] Q = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(bc) ] + [c(ab) + c(ac) + c(cb)]](/latexrender/pictures/f7b1996e7a71532fe87986ec2566c5e4.png) e add
e add 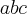 nos dois lados da igualdade
nos dois lados da igualdade ![Q +abc = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(ac)+ b(bc) ] + [c(ab) + c(ac) + c(cb)] Q +abc = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(ac)+ b(bc) ] + [c(ab) + c(ac) + c(cb)]](/latexrender/pictures/44f06630283829a20ee3f2a62ce46c6d.png) e assim obtemos
e assim obtemos  e portanto
e portanto 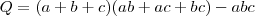

teremos
(1) (muito obrigado Wolfram alpha ! ) ,agorá é só "brincar" com os a,b,c de modo a usar as Relações de Girard que estabelece uma relação entre as raízes de um polinômio e os seus coeficientes . De acordo com estas relações ,dada equação polinomial
cuja raízes reais são
,temos os resultados :
.
, segue
e add
nos dois lados da igualdade
e assim obtemos
e portanto

