Digitei-a no WolframAlpha, mas não deu a resolução sob a fórmula algébrica, mas apenas através de gráficos, e apresentou as seguinte fórmulas:
Fórmula alternativa:
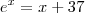
Soluções reais ___ Formas aproximadas:
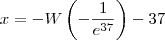
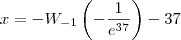
Solução ___ Forma aproximada:
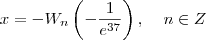
Solução ___ Forma exacta:
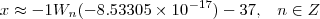
Valores na Recta Real (o)
_O_______________________________________________O__
Pelo que andei pesquisando na net o
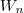é chamado de função 
de Lambert, que é usada para resolver equações transcendentais. Achei a coisa demasiado complicada, pois é preciso aplicar logaritmos em ambos os lados da equação. Ou pode ser apenas impressão minha, dado que não estou familiarizado com a dita função,aliás, nem nunca tinha ouvido falar.Será que a equação que postei só pode ser mesmo resolvida por aquele método ? Não haverá um processo mais fácil ?
Agradecia ajuda dentro do possível.
Att.
Armando
.
: