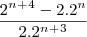
O que eu fiz foi somar os expoentes, ficando assim:
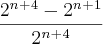
Agora cortei o 2^n+4 , Ficando assim:

Porém, o resultado do gabarito é totalmente diferente...
Resultado é:

Qual foi meu erro?, Confundi alguma propriedade?...

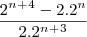
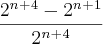







Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante