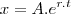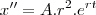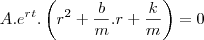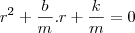Eu faço também a disciplina EDO, mas até o momento eu aprendi: Quadratura, Mudança de variáveis, PVI, aplicações, equações homogêneas de classe A e C.
Foi nos dado a seguinte EDO:
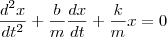
Não me recordo de ter aprendido tal EDO e nem mesmo sei o nome dela.
Com o que eu aprendi até o momento, eu consigo resolvê-la?
Alguém pode me ajudar nessa EDO?
Obrigado.