 por Tixa11 » Sex Jan 25, 2013 20:28
por Tixa11 » Sex Jan 25, 2013 20:28
Como resolvo?

Obrigado.
-
Tixa11
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Sáb Nov 10, 2012 12:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bioquimica
- Andamento: cursando
 por young_jedi » Sáb Jan 26, 2013 12:07
por young_jedi » Sáb Jan 26, 2013 12:07
utilize o metodo do fator integrante
ou então
divida a equação por x

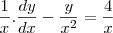
utilizando a regra da cadeia podemos dizer que

portanto

integrando a equação com relação a x temos
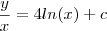

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



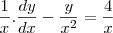


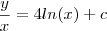



 .
.



