 por RafaelPereira » Dom Dez 02, 2012 20:36
por RafaelPereira » Dom Dez 02, 2012 20:36
-
RafaelPereira
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Dom Dez 02, 2012 17:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Dom Dez 02, 2012 22:05
por e8group » Dom Dez 02, 2012 22:05
Note que ,
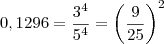
.
Reescrevendo a equação da seguinte forma ,
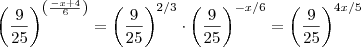
.
Multiplicando ambos lados por ,
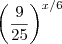
. Vamos obter ,

.
Uma vez que as bases são iguais (e fixas) temos que seus respectivos expoentes são iguais ,então :
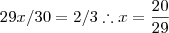
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por RafaelPereira » Seg Dez 03, 2012 00:50
por RafaelPereira » Seg Dez 03, 2012 00:50
Obrigado santhiago, pois pela sua resposta acabei percebendo qual foi o ponto em que eu estava errando e fazendo com que eu não achasse a solução.
Eu estava escrevendo a expressão
![{\left(\sqrt[5]{0,1296} \right)}^{2x} {\left(\sqrt[5]{0,1296} \right)}^{2x}](/latexrender/pictures/8b5f81037744529f248b690f595f9473.png)
, da forma
![{\left(\sqrt[5]{\frac{1296}{1000}} \right)}^{2x} = {\left(\sqrt[5]{\frac{{2}^{4}.{3}^{4}}{{2}^{3}.{5}^{3}}} \right)}^{2x} {\left(\sqrt[5]{\frac{1296}{1000}} \right)}^{2x} = {\left(\sqrt[5]{\frac{{2}^{4}.{3}^{4}}{{2}^{3}.{5}^{3}}} \right)}^{2x}](/latexrender/pictures/88e8d5d99596ada8e194968b8c6c4410.png)
,o que está errado. A forma correta é
![{\left(\sqrt[5]{\frac{1296}{10000}} \right)}^{2x} = {\left(\sqrt[5]{\frac{{2}^{4}.{3}^{4}}{{2}^{4}.{5}^{4}}} \right)}^{2x} = {\left(\sqrt[5]{\frac{{3}^{4}}{{5}^{4}}} \right)}^{2x} = {\left[\sqrt[5]{{\left(\frac{9}{25} \right)}^{2}} \right]}^{2x} {\left(\sqrt[5]{\frac{1296}{10000}} \right)}^{2x} = {\left(\sqrt[5]{\frac{{2}^{4}.{3}^{4}}{{2}^{4}.{5}^{4}}} \right)}^{2x} = {\left(\sqrt[5]{\frac{{3}^{4}}{{5}^{4}}} \right)}^{2x} = {\left[\sqrt[5]{{\left(\frac{9}{25} \right)}^{2}} \right]}^{2x}](/latexrender/pictures/a0a8e8b1d05c31c88f090263499d4574.png)
.
Agora refiz os cálculos e bateu exatamente com o que você disse.
Vlw. Muito Obrigado.
-
RafaelPereira
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Dom Dez 02, 2012 17:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação com Radical
por LAYLA » Qui Jun 07, 2018 21:14
- 1 Respostas
- 13746 Exibições
- Última mensagem por Gebe

Sáb Jun 09, 2018 10:28
Sistemas de Equações
-
- [função exponencial] Uma dúvida sobre equações exponenciais.
por amyss » Qui Jul 05, 2012 22:37
- 1 Respostas
- 1388 Exibições
- Última mensagem por Russman

Qui Jul 05, 2012 23:06
Funções
-
- Duvida Op. Radical
por Andrewo » Seg Mar 05, 2012 11:09
- 1 Respostas
- 2058 Exibições
- Última mensagem por MarceloFantini

Seg Mar 05, 2012 13:13
Álgebra Elementar
-
- Radical Duplo
por Rafael16 » Seg Jan 21, 2013 20:40
- 2 Respostas
- 3779 Exibições
- Última mensagem por Rafael16

Seg Jan 21, 2013 20:53
Aritmética
-
- Radical duplo
por Maria Livia » Sex Fev 22, 2013 00:10
- 1 Respostas
- 14308 Exibições
- Última mensagem por DanielFerreira

Sex Fev 22, 2013 01:11
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{\sqrt[3]{{\left(\frac{9}{25} \right)}^{-x+4}}}={\left(\sqrt[5]{0,1296} \right)}^{2x} \sqrt[]{\sqrt[3]{{\left(\frac{9}{25} \right)}^{-x+4}}}={\left(\sqrt[5]{0,1296} \right)}^{2x}](/latexrender/pictures/f54b6293c90c66119912310b633f123a.png)
![\sqrt[6]{{\left(\frac{{3}^{2}}{{5}^{2}} \right)}^{-x+4}}={\left(\sqrt[5]{\frac{{2}^{4}.{3}^{4}}{{2}^{3}.{5}^{3}}}} \right)^{2x} \sqrt[6]{{\left(\frac{{3}^{2}}{{5}^{2}} \right)}^{-x+4}}={\left(\sqrt[5]{\frac{{2}^{4}.{3}^{4}}{{2}^{3}.{5}^{3}}}} \right)^{2x}](/latexrender/pictures/0189d7f3ce5beda652504a18ec002405.png)
![\sqrt[6]{{\left(\frac{3}{5} \right)}^{2\left(-x+4 \right)}}={\left(\sqrt[5]{\frac{{\left(2.3 \right)}^{4}}{{\left(2.5 \right)}^{3}}} \right)}^{2x} \sqrt[6]{{\left(\frac{3}{5} \right)}^{2\left(-x+4 \right)}}={\left(\sqrt[5]{\frac{{\left(2.3 \right)}^{4}}{{\left(2.5 \right)}^{3}}} \right)}^{2x}](/latexrender/pictures/c9bb6d9d3e8e7796c4a09d370b9b9c83.png)
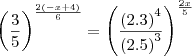

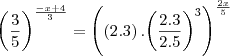
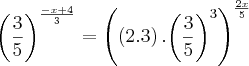

![\sqrt[]{\sqrt[3]{{\left(\frac{9}{25} \right)}^{-x+4}}}={\left(\sqrt[5]{0,1296} \right)}^{2x} \sqrt[]{\sqrt[3]{{\left(\frac{9}{25} \right)}^{-x+4}}}={\left(\sqrt[5]{0,1296} \right)}^{2x}](/latexrender/pictures/f54b6293c90c66119912310b633f123a.png)
![\sqrt[6]{{\left(\frac{{3}^{2}}{{5}^{2}} \right)}^{-x+4}}={\left(\sqrt[5]{\frac{{2}^{4}.{3}^{4}}{{2}^{3}.{5}^{3}}}} \right)^{2x} \sqrt[6]{{\left(\frac{{3}^{2}}{{5}^{2}} \right)}^{-x+4}}={\left(\sqrt[5]{\frac{{2}^{4}.{3}^{4}}{{2}^{3}.{5}^{3}}}} \right)^{2x}](/latexrender/pictures/0189d7f3ce5beda652504a18ec002405.png)
![\sqrt[6]{{\left(\frac{3}{5} \right)}^{2\left(-x+4 \right)}}={\left(\sqrt[5]{\frac{{\left(2.3 \right)}^{4}}{{\left(2.5 \right)}^{3}}} \right)}^{2x} \sqrt[6]{{\left(\frac{3}{5} \right)}^{2\left(-x+4 \right)}}={\left(\sqrt[5]{\frac{{\left(2.3 \right)}^{4}}{{\left(2.5 \right)}^{3}}} \right)}^{2x}](/latexrender/pictures/c9bb6d9d3e8e7796c4a09d370b9b9c83.png)
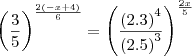

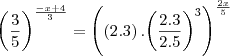
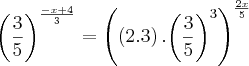

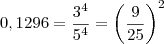 .
. 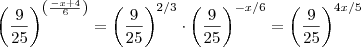 .
. 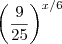 . Vamos obter ,
. Vamos obter ,  .
. 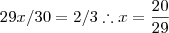 .
.
![{\left(\sqrt[5]{0,1296} \right)}^{2x} {\left(\sqrt[5]{0,1296} \right)}^{2x}](/latexrender/pictures/8b5f81037744529f248b690f595f9473.png) , da forma
, da forma ![{\left(\sqrt[5]{\frac{1296}{1000}} \right)}^{2x} = {\left(\sqrt[5]{\frac{{2}^{4}.{3}^{4}}{{2}^{3}.{5}^{3}}} \right)}^{2x} {\left(\sqrt[5]{\frac{1296}{1000}} \right)}^{2x} = {\left(\sqrt[5]{\frac{{2}^{4}.{3}^{4}}{{2}^{3}.{5}^{3}}} \right)}^{2x}](/latexrender/pictures/88e8d5d99596ada8e194968b8c6c4410.png) ,o que está errado. A forma correta é
,o que está errado. A forma correta é ![{\left(\sqrt[5]{\frac{1296}{10000}} \right)}^{2x} = {\left(\sqrt[5]{\frac{{2}^{4}.{3}^{4}}{{2}^{4}.{5}^{4}}} \right)}^{2x} = {\left(\sqrt[5]{\frac{{3}^{4}}{{5}^{4}}} \right)}^{2x} = {\left[\sqrt[5]{{\left(\frac{9}{25} \right)}^{2}} \right]}^{2x} {\left(\sqrt[5]{\frac{1296}{10000}} \right)}^{2x} = {\left(\sqrt[5]{\frac{{2}^{4}.{3}^{4}}{{2}^{4}.{5}^{4}}} \right)}^{2x} = {\left(\sqrt[5]{\frac{{3}^{4}}{{5}^{4}}} \right)}^{2x} = {\left[\sqrt[5]{{\left(\frac{9}{25} \right)}^{2}} \right]}^{2x}](/latexrender/pictures/a0a8e8b1d05c31c88f090263499d4574.png) .
.