 por Debylow » Ter Nov 13, 2012 18:06
por Debylow » Ter Nov 13, 2012 18:06
Creio que seja facil , mas quem puder me responder eu agradeço .
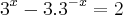
e essa outra
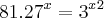
-
Debylow
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Nov 13, 2012 17:37
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por e8group » Ter Nov 13, 2012 19:12
por e8group » Ter Nov 13, 2012 19:12
Na primeira, multiplica toda equação por

em seguida soma
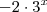
dois lados da equação e faça

, resolva para

, volte e resolva para

. Ressaltando que
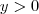
.
Na segunda equação é importante perceber que
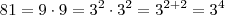
e
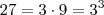
. diante disso você terá que as bases são iguais , como elas são fixas , então o expoente delas tem de ser iguais para satisfazer a igualdade .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Debylow » Ter Nov 13, 2012 20:36
por Debylow » Ter Nov 13, 2012 20:36
[quote="santhiago"]Na primeira, multiplica toda equação por

em seguida soma
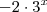
dois lados da equação e faça

, resolva para

, volte e resolva para

. Ressaltando que
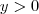
.
continuo sem entender essa , obg por me responder, entendi a 2°
-
Debylow
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Nov 13, 2012 17:37
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por MarceloFantini » Ter Nov 13, 2012 20:54
por MarceloFantini » Ter Nov 13, 2012 20:54
Multiplicando tudo por

temos
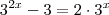
. Faça a substituição
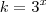
. Segue que
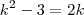
. Termine.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Debylow » Qua Nov 14, 2012 11:32
por Debylow » Qua Nov 14, 2012 11:32
continuo sem entender a equação , algumas partes eu entendi (onde tem que trocar por K) mas como chega até la que nao entendi . mesmo assim obg. Mas quem puder fazer ela toda acho melhor pra tirar minha dúvida .
-
Debylow
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Nov 13, 2012 17:37
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por e8group » Qua Nov 14, 2012 12:23
por e8group » Qua Nov 14, 2012 12:23
Multiplicando toda equação por

e fazendo

obtemos ,
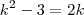
.Somando
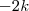
nos dois lados da igualdade ,
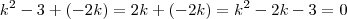
.Equação do segundo grau , consegue resolver por
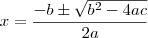
? Basta aplicar a esta equação . Depois volte para

e resolva . Lembrando que

-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Debylow » Qua Nov 14, 2012 12:42
por Debylow » Qua Nov 14, 2012 12:42
Finalmente entendi . só me explica por que tenho que multiplicar tudo por

e depois tenho que somar -2K dos dois lados! valeu msm
-
Debylow
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Nov 13, 2012 17:37
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- problema simples de operações com números naturais - EF
por juliahess » Ter Jul 31, 2012 12:55
- 1 Respostas
- 1275 Exibições
- Última mensagem por DanielFerreira

Ter Jul 31, 2012 21:26
Álgebra Elementar
-
- Uma equação e duas incognitas
por gokeafro » Sex Out 14, 2011 22:39
- 1 Respostas
- 1450 Exibições
- Última mensagem por MarceloFantini

Sáb Out 15, 2011 11:41
Sistemas de Equações
-
- equação com duas variaveis
por celita » Qui Jul 28, 2016 23:34
- 1 Respostas
- 3366 Exibições
- Última mensagem por Daniel Bosi

Sex Jul 29, 2016 09:37
Equações
-
- [Equação de reta] - duas dúvidas
por MrJuniorFerr » Sex Out 12, 2012 22:03
- 3 Respostas
- 1771 Exibições
- Última mensagem por young_jedi

Sáb Out 13, 2012 11:14
Geometria Analítica
-
- Equação geral do plano usando duas retas
por iarapassos » Sáb Set 01, 2012 19:12
- 2 Respostas
- 8779 Exibições
- Última mensagem por iarapassos

Dom Set 02, 2012 22:15
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
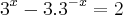 e essa outra
e essa outra 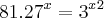

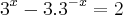 e essa outra
e essa outra 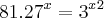

 em seguida soma
em seguida soma 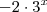 dois lados da equação e faça
dois lados da equação e faça  , resolva para
, resolva para  , volte e resolva para
, volte e resolva para  . Ressaltando que
. Ressaltando que 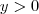 .
. 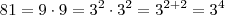 e
e 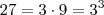 . diante disso você terá que as bases são iguais , como elas são fixas , então o expoente delas tem de ser iguais para satisfazer a igualdade .
. diante disso você terá que as bases são iguais , como elas são fixas , então o expoente delas tem de ser iguais para satisfazer a igualdade .
 em seguida soma
em seguida soma 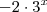 dois lados da equação e faça
dois lados da equação e faça  , resolva para
, resolva para  , volte e resolva para
, volte e resolva para  . Ressaltando que
. Ressaltando que 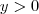 .
. 
 temos
temos 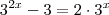 . Faça a substituição
. Faça a substituição 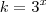 . Segue que
. Segue que 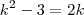 . Termine.
. Termine.


 e fazendo
e fazendo  obtemos ,
obtemos , 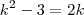 .Somando
.Somando 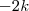 nos dois lados da igualdade ,
nos dois lados da igualdade , 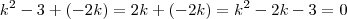 .Equação do segundo grau , consegue resolver por
.Equação do segundo grau , consegue resolver por 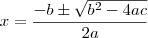 ? Basta aplicar a esta equação . Depois volte para
? Basta aplicar a esta equação . Depois volte para  e resolva . Lembrando que
e resolva . Lembrando que 

 e depois tenho que somar -2K dos dois lados! valeu msm
e depois tenho que somar -2K dos dois lados! valeu msm


 , avisa que eu resolvo.
, avisa que eu resolvo.

