Ajuda equação de 2º grau

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Ajuda equação de 2º grau

Regras do fórum
Responder

Ajuda equação de 2º grau

Mensagempor MarceloFantini » Ter Ago 28, 2012 19:22

Seja P o preço por bola e Q a quantidade de bolas, pela primeira informação temos que P \cdot Q = 400.

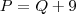A segunda informação diz que se o preço fosse 4 reais a menos a quantidade seria de 5 a mais, em símbolos traduzimos como P -4 = Q+5. Temos um sistema de equações para resolver, de onde podemos isolar o preço como P = Q+9 e substituir na primeira, fazendo P \cdot Q = (Q+9) \cdot Q = Q^2 +9Q = 400.

As soluções são 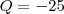Q = -25, que é descartada pois sabemos que o número de bolas é maior que zero, e Q=16.

Note que isso significa que o preço de cada bola seria 25 reais. No cenário em que você propôs teríamos 20 bolas custando 20 reais cada, mas isto não satisfaz a segunda equação, pois 20-4 não é igual a 20+5, ou seja, você não satisfaz a condição do enunciado! Portanto não pode ser solução.
Futuro MATEMÁTICO
e^{\pi \cdot i} +1 = 0
MarceloFantini
Colaborador Moderador
Colaborador Moderador
 
Mensagens: 3126
Registrado em: Seg Dez 14, 2009 11:41
Formação Escolar: GRADUAÇÃO
Andamento: formado
Voltar ao topo
Responder

Voltar para Equações

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: [Função] do primeiro grau e quadratica
Autor: Thassya - Sáb Out 01, 2011 16:20

1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?

2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?

3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?

Assunto: [Função] do primeiro grau e quadratica
Autor: Neperiano - Sáb Out 01, 2011 19:46

Ola

Qual as suas dúvidas?

O que você não está conseguindo fazer?

Nos mostre para podermos ajudar

Atenciosamente

Assunto: [Função] do primeiro grau e quadratica
Autor: joaofonseca - Sáb Out 01, 2011 20:15

1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.

y_{b}-y_{a}=m(x_{b}-x_{a})

1-3=m(-3-1) \Leftrightarrow -2=-4m \Leftrightarrow m=\frac{2}{4} \Leftrightarrow m=\frac{1}{2}

Em y=mx+b substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.

3=\frac{1}{2} \cdot 1+b\Leftrightarrow 3-\frac{1}{2}=b \Leftrightarrow b=\frac{5}{2}



2)Na equação y=x^2-5x+9 não existem zeros.Senão vejamos

Completando o quadrado,

(x^2-5x+\frac{25}{4})+9-\frac{25}{4} =0\Leftrightarrow (x-\frac{5}{2})^2+\frac{11}{4}=0

As coordenadas do vertice da parabola são (\frac{5}{2},\frac{11}{4})

O eixo de simetria é a reta x=\frac{5}{2}.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.

f(-7)=93
f(10)=59

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum