Estou com dúvida na seguinte questão:
'As casas do quadrado da figura abaixo foram preenchidas com nove números inteiros positivos, de modo a fazer com que os produtos dos números de cada linha, de cada coluna e de cada diagonal fossem todos iguais.
Em seguida, seis números inteiros foram apagados, restando os números 6, 9 e 12, nas posições mostradas. Se x era o número escrito na casa que está na primeira linha e na primeira coluna, e y era o número escrito na casa que está na primeira linha e na terceira coluna, qual o valor de x + y?'
- imagem.PNG (2.47 KiB) Exibido 1320 vezes
A resposta correta é 5.
Analisando a diagonal principal e a terceira coluna, vê-se que a igualdade do produto de seus respectivos números acontece para valores de x e y satisfazendo 2x = 3y, no entanto, não consegui estabelecer a unicidade do resultado, satisfazendo a igualdade dos produtos de todas as linhas colunas e diagonais......
Obrigado.
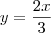, que será inteiro apenas se 
com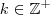 
.
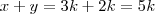. A menor solução será se 
, daí a resposta. Se ele dissesse que 12 era o maior número inteiro positivo dentre os que estão no quadrado conseguiríamos a unicidade deste resultado, mas não sei de que outra forma isto é possível.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.