Número primo
[...]
Para todo primo p seja p# o produto de todos os números
primos q inferiores ou iguais a p. De acordo com a terminologia
empregada por Dubner (1987), p# é chamado o primorial de p.[...]
Dadas as afirmativas sobre primoriais de números primos,
considerando estritamente a definição e a simbologia
estabelecidas no texto,
I. O primorial de um número primo é um número primo.
II. Se p é um número primo maior que 2, a soma dos algarismos
do número p# + 3 é um número múltiplo de 3.
III. 8# = 2x3x5x7 = 210.
verifica-se que está(ão) correta(s)
A) I, II e III.
B) I e III, apenas.
C) I e II, apenas.
D) III, apenas.
E) II, apenas.
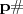(primordial) é o produto dos números primos menores ou iguais a 
. Assim, como exemplo, podemos tomar qualquer primo. Seja 
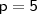, daí,
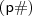será um múltiplo de 3, com efeito, 
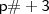também será múltiplo de 3.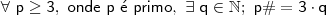
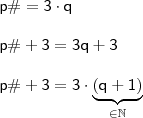
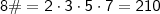
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.