-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477961 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 530165 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 493750 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 701049 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2113036 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por sony » Qua Jun 15, 2016 20:48
por sony » Qua Jun 15, 2016 20:48
GOSTARIA MUITO QUE VOCÊS- ME AJUDASSEM NESSES EXERCÍCIOS;
Marcos comprou um carro zero quilômetro e quer fazer o controle do consumo de combustível de seu carro. Observou que, com 33 L de gasolina, ele pode rodar 95 m na
cidade mais 276 m na estrada e que, com 42 L de gasolina, ele pode rodar 190 m na cidade mais 264 km na estrada.
1 . De acordo com as informações do texto , calcule quantos quilômetros Marcos pode rodar na cidade com 1 L de gasolina.
a. 9,5 Km
b. 9,0 Km
c. 8,5 Km
d. 8,0 Km
2. Sabendo-se que Marcos viajou 143,5 Km com 13 L de gasolina, determine quantos quilômetros ele percorreu.
a. 90 Km
b. 96 Km
c. 98 Km
d. 103 Km
-
sony
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jun 15, 2016 20:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por adauto martins » Ter Jun 21, 2016 19:37
por adauto martins » Ter Jun 21, 2016 19:37
a)
aqui é resolver o
sistema:
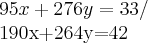
,onde x,y sao medidos em (l/km)
b)
aqui usa-se o valor calculado de y,acima...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- problema de matematica
por verinha72 » Qua Out 06, 2010 23:24
- 1 Respostas
- 3028 Exibições
- Última mensagem por Elcioschin

Qui Out 07, 2010 17:57
Mensagens Matemáticas
-
- PROBLEMA DE MATEMÁTICA
por deiabae » Seg Ago 08, 2011 22:41
- 1 Respostas
- 2633 Exibições
- Última mensagem por Molina

Seg Ago 08, 2011 22:57
Funções
-
- problema de matematica
por orlene » Qui Set 15, 2011 13:43
- 1 Respostas
- 1618 Exibições
- Última mensagem por MarceloFantini

Qui Set 15, 2011 16:17
Matemática Financeira
-
- Problema de Matemática
por elmanoduarte » Qui Dez 01, 2011 10:29
- 1 Respostas
- 1333 Exibições
- Última mensagem por elmanoduarte

Qui Dez 01, 2011 20:57
Cálculo: Limites, Derivadas e Integrais
-
- problema de matemática 01
por leonardo151273 » Qua Mar 21, 2012 23:18
- 1 Respostas
- 1695 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 19, 2012 14:45
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


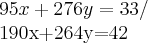 ,onde x,y sao medidos em (l/km)
,onde x,y sao medidos em (l/km)