Eu sempre realizei minhas contas de frações de maneira simples, ortodoxa como aprendi na escola usando mmc, divide e multiplica. Porém, eu navegando nos vídeos do youtube me deparei com um professor ensinando a calcular frações sem usar mmc e isso é novo pra mim, nunca vi ninguém usar dessa maneira, mas todas as vezes que tentei deu certo. Porém eu perco tempo, sempre verifico depois da maneira que sempre fiz antes. Porisso eu quero saber se essa regrinha é válida em todos os casos. Basicamente você multiplica os denominadores , deixa o resultado no denominador, multiplica as frações em cruz respeitado os sinais e o resultado vai para o numerador
Não há nada de errado em ambos métodos. Na verdade são a mesma operação.
De fato, dadas duas frações e com b e de nulos a sua soma é
Esta é a forma algébrica de soma de frações. Assim que o professor ensina no vídeo.
O processo de mmc otimiza o processo de soma.
Veja que uma vez tomando a base da soma como o mmc entre as duas bases não é necessário simplificar o resultado, coisa que, por vezes, ocorre no processo dito acima.
Por exemplo: algebricamente, a soma
é
Agora, a fração pode ser simplificada para
.
Agora, se você calcular o mmc entre as bases, isto é, , chega ao resultado tendo que trabalhar com números menores.
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é
Alguem me ajuda? Agradeço desde já.
Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:
Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:
Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:
e 
com b e de nulos a sua soma é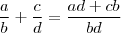
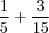
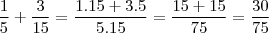
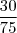pode ser simplificada para 
.
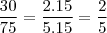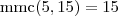, chega ao resultado tendo que trabalhar com números menores.
